题目内容
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.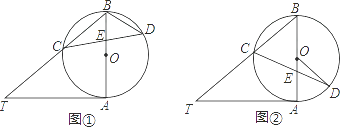
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
【答案】
(1)解:如图①,连接AC,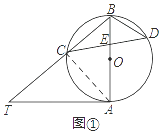
∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°﹣∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°﹣∠ABC=40°,
∴∠CDB=∠CAB=40°
(2)解:如图②,连接AD,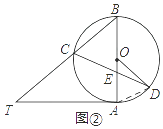
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA﹣∠ADC=65°﹣50°=15°
【解析】(1)连接AC,根据圆的切线垂直于经过切点的半径可得∠TAB=90°,由已知条件可求得∠T和∠CDB的度数。
(2)连接AD,在△BCE中,根据已知条件:BE=BC,∠EBC=50°,可求得∠BCE=∠BEC=65°,由同弧所对的圆周角相等可得∠BAD=∠BCD=65°,再根据等边对等角得∠ODA=∠OAD=65°,∠CDO=∠ODA﹣∠ADC,∠CDO的度数可求。

【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.