题目内容
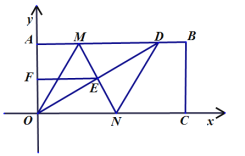
【题目】如图，在平面直角坐标系中，已知矩形AOCB的顶点O、A的坐标分别是（0，0）、（0，a），且满足
． 点D是AB上一点， M，N垂直平分OD，分别交AB，OD，OC于点M，E，N，连接OM，DN．
（1）填空：a = ；
（2）求证：四边形MOND是菱形；
（3）若F为OA的中点，连接EF，且满足EF+OE=9，求四边形MOND的周长和面积．
【答案】（1）6；（2）详见解析；（3）C菱形MOND=25，S菱形MOND=
【解析】
（1）根据二次根式的非负性进行求解即可；
（2）根据矩形AOCB的性质以及
判定四边形MOND是平行四边形，再由菱形的判定求证即可；
（3）根据
的中位线及矩形AOCB的性质构造直角三角形，设AD=x，
利用勾股定理求出x的值，再根据菱形MOND的性质，设
，
，利用勾股定理求出y，最后根据菱形的周长及面积求法进行求解即可.
（1）∵
∴
，
∴
∴
；
（2）证明：∵MN垂直平分OD
∴OM=DM，DE=OE，
∵四边形AOCB是矩形
∴AB∥OC
∴
在
和
中
∴
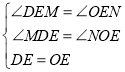
∴ME=NE
又∵DE=OE
∴四边形MOND是平行四边形
又∵OM=DM
∴四边形MOND是菱形；
（3）由（1）得OA=6
由（2）得DE=OE
又∵F为OA的中点
∴EF是的中位线，
∴
又∵EF+OE=9，DE=OE
∴
∴AD+OD =18
∵四边形AOCB是矩形
∴
在
中
设AD=x，则
根据勾股定理，
，解得x=8
∴AD=8，OD =10
由（2）得，四边形MOND是菱形
∴OM=MD=DN=ON
设，则
在
中，根据勾股定理
，解得
∴
∴
，
.
练习册系列答案
相关题目
