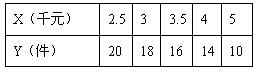题目内容
某公司新进一批商品，每件商品进价2000元，为了解该商品的销售情况，公司统计了该商品一段时间内日销售单价x（千元）和日销售y件）的数据如下：| x （千元） | 2.5 | 3 | 3.5 | 4 | 5 |
| y（件） | 20 | 18 | 16 | 14 | 10 |
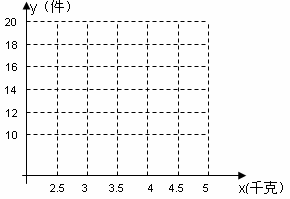
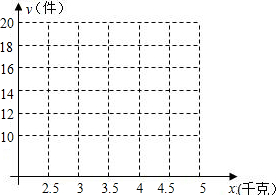
①据表中提供的数据描出实数对（x，y）；
②根据①，猜测并确定日销售量y（件）与日销售单价x（千元）之间的函数关系式；
（II）设日销售利润L千元（利润=收入-成本，其他因素不考虑），写出L与x的函数关系式，并回答：当x为何值时，日销售利润L有最大值，最大值是多少？日销售利润L有最小值吗？如果有，是多少？
分析：待定系数法求一次函数解析式，利用利润=收入-成本列出表达式，整理就可以得到函数解析式，求二次函数的最值问题．
解答：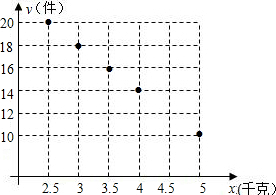
解：（1）设函数关系式为y=kx+b，则
，
解得
，
∴y=-4x+30；
（2）L=xy-2y=y（x-2）=（x-2）（-4x+30）=-4x2+38x-60，
∵a=-4＜0，
∴L有最大值，最大值为
=30.25千元，
没有最小值．
解：（1）设函数关系式为y=kx+b，则
|
解得
|
∴y=-4x+30；
（2）L=xy-2y=y（x-2）=（x-2）（-4x+30）=-4x2+38x-60，
∵a=-4＜0，
∴L有最大值，最大值为
| 4(-4)(-60)-382 |
| 4(-4) |
没有最小值．
点评：本题主要考查待定系数法和二次函数的最值问题，二次函数的最值问题可以用公式法、也可以用配方法求解．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
某公司新进一批商品，每件商品进价2000元，为了解该商品的销售情况，公司统计了该商品一段时间内日销售单价x（千元）和日销售y件）的数据如下：
| x （千元） | 2.5 | 3 | 3.5 | 4 | 5 |
| y（件） | 20 | 18 | 16 | 14 | 10 |
①据表中提供的数据描出实数对（x，y）；
②根据①，猜测并确定日销售量y（件）与日销售单价x（千元）之间的函数关系式；
（II）设日销售利润L千元（利润=收入-成本，其他因素不考虑），写出L与x的函数关系式，并回答：当x为何值时，日销售利润L有最大值，最大值是多少？日销售利润L有最小值吗？如果有，是多少？
（2004•日照）某公司新进一批商品，每件商品进价2000元，为了解该商品的销售情况，公司统计了该商品一段时间内日销售单价x（千元）和日销售y件）的数据如下：
（I）在所给的直角坐标系中
①据表中提供的数据描出实数对（x，y）；
②根据①，猜测并确定日销售量y（件）与日销售单价x（千元）之间的函数关系式；
（II）设日销售利润L千元（利润=收入-成本，其他因素不考虑），写出L与x的函数关系式，并回答：当x为何值时，日销售利润L有最大值，最大值是多少？日销售利润L有最小值吗？如果有，是多少？
| x （千元） | 2.5 | 3 | 3.5 | 4 | 5 |
| y（件） | 20 | 18 | 16 | 14 | 10 |
①据表中提供的数据描出实数对（x，y）；
②根据①，猜测并确定日销售量y（件）与日销售单价x（千元）之间的函数关系式；
（II）设日销售利润L千元（利润=收入-成本，其他因素不考虑），写出L与x的函数关系式，并回答：当x为何值时，日销售利润L有最大值，最大值是多少？日销售利润L有最小值吗？如果有，是多少？
（2004•日照）某公司新进一批商品，每件商品进价2000元，为了解该商品的销售情况，公司统计了该商品一段时间内日销售单价x（千元）和日销售y件）的数据如下：
（I）在所给的直角坐标系中
①据表中提供的数据描出实数对（x，y）；
②根据①，猜测并确定日销售量y（件）与日销售单价x（千元）之间的函数关系式；
（II）设日销售利润L千元（利润=收入-成本，其他因素不考虑），写出L与x的函数关系式，并回答：当x为何值时，日销售利润L有最大值，最大值是多少？日销售利润L有最小值吗？如果有，是多少？
| x （千元） | 2.5 | 3 | 3.5 | 4 | 5 |
| y（件） | 20 | 18 | 16 | 14 | 10 |
①据表中提供的数据描出实数对（x，y）；
②根据①，猜测并确定日销售量y（件）与日销售单价x（千元）之间的函数关系式；
（II）设日销售利润L千元（利润=收入-成本，其他因素不考虑），写出L与x的函数关系式，并回答：当x为何值时，日销售利润L有最大值，最大值是多少？日销售利润L有最小值吗？如果有，是多少？