题目内容
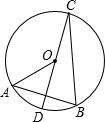
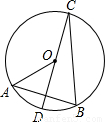
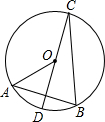如图在⊙O中，直径CD⊥弦AB，且∠AOD=60°，则∠DCB的度数是________°．
30
分析：由于CD⊥AB，根据垂径定理可知弧AD=弧BD，从而可知∠AOD=∠BOD=60°，再结合圆周角定理易求∠DCB．
解答：
解：如右图，连接OB，
∵CD⊥AB，
∴弧AD=弧BD，
∴∠AOD=∠BOD=60°，
∴∠BCD=
∠BOD=×60°=30°．
故答案是30°．
点评：本题考查了垂径定理、圆周角定理，解题的关键是连接OB．
分析：由于CD⊥AB，根据垂径定理可知弧AD=弧BD，从而可知∠AOD=∠BOD=60°，再结合圆周角定理易求∠DCB．
解答：
解：如右图，连接OB，∵CD⊥AB，
∴弧AD=弧BD，
∴∠AOD=∠BOD=60°，
∴∠BCD=
∠BOD=×60°=30°．故答案是30°．
点评：本题考查了垂径定理、圆周角定理，解题的关键是连接OB．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
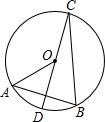如图在⊙O中，直径CD⊥弦AB，且∠AOD=60°，则∠DCB的度数是
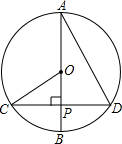如图在⊙O中，直径AB⊥弦CD，垂足为P，∠BAD=30°，则∠AOC的度数是
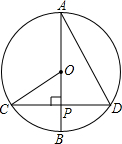如图在⊙O中，直径AB⊥弦CD，垂足为P，∠BAD=30°，则∠AOC的度数是________度．
