题目内容
已知二次函数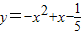 ,当自变量x取m时对应的值大于0,当自变量x分别取m-1、m+1时对应的函数值为y1、y2,则y1、y2必须满足( )
,当自变量x取m时对应的值大于0,当自变量x分别取m-1、m+1时对应的函数值为y1、y2,则y1、y2必须满足( )A.y1>0、y2>0
B.y1<0、y2<0
C.y1<0、y2>0
D.y1>0、y2<0
【答案】分析:根据函数的解析式求得函数与x轴的交点坐标,利用自变量x取m时对应的值大于0,确定m-1、m+1的位置,进而确定函数值为y1、y2.
解答:解:令 =0,
=0,
解得:x= ,
,
∵当自变量x取m时对应的值大于0,
∴ <m<
<m< ,
,
∵点(m+1,0)与(m-1,0)之间的距离为2,大于二次函数与x轴两交点之间的距离,
∴m-1的最大值在左边交点之左,m+1的最小值在右边交点之右.
∴点(m+1,0)与(m-1,0)均在交点之外,
∴y1<0、y2<0.
故选B.
点评:本题考查了抛物线与x轴的交点和二次函数图象上的点的特征,解题的关键是求得抛物线与横轴的交点坐标.
解答:解:令
 =0,
=0,解得:x=
 ,
,∵当自变量x取m时对应的值大于0,
∴
 <m<
<m< ,
,∵点(m+1,0)与(m-1,0)之间的距离为2,大于二次函数与x轴两交点之间的距离,
∴m-1的最大值在左边交点之左,m+1的最小值在右边交点之右.
∴点(m+1,0)与(m-1,0)均在交点之外,
∴y1<0、y2<0.
故选B.
点评:本题考查了抛物线与x轴的交点和二次函数图象上的点的特征,解题的关键是求得抛物线与横轴的交点坐标.

练习册系列答案
相关题目
已知二次函数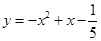 ,当自变量
,当自变量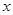 取
取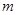 时,对应的函数值大于0,当自变量
时,对应的函数值大于0,当自变量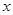 分别取
分别取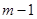 ,
,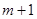 时对应的函数值
时对应的函数值 、
、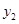 ,则
,则 ,
,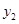 满足
满足
A. >0, >0,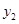 >0 >0 | B. <0, <0,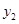 <0 <0 | C. <0, <0,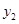 >0 >0 | D. >0, >0,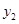 <0 <0 |
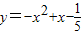 ,当自变量x取m时对应的值大于0,当自变量x分别取m-1、m+1时对应的函数值为y1、y2,则y1、y2必须满足( )
,当自变量x取m时对应的值大于0,当自变量x分别取m-1、m+1时对应的函数值为y1、y2,则y1、y2必须满足( ) ,当自变量
,当自变量 取
取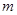 时,对应的函数值大于0,当自变量
时,对应的函数值大于0,当自变量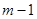 ,
, 时对应的函数值
时对应的函数值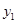 、
、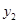 ,则
,则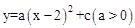 ,当自变量x分别取
,当自变量x分别取 ,3,0时,对应的值分别为
,3,0时,对应的值分别为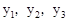 ,则
,则 B.
B. 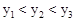 C.
C.
 D.
D.
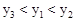
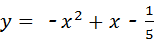 ,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2,则y1、y2必须满足( )
,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2,则y1、y2必须满足( )