题目内容
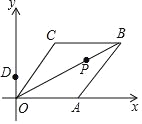
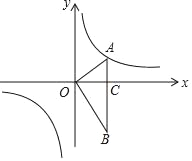
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上是否存在一点P,使得S△AOP=![]() S△AOB,若存在,求所有符合条件点P的坐标;若不存在,简述你的理由.
S△AOB,若存在,求所有符合条件点P的坐标;若不存在,简述你的理由.
【答案】(1)y=![]() ;(2)(﹣2
;(2)(﹣2![]() ,0)或(2
,0)或(2![]() ,0)
,0)
【解析】
(1)把A的坐标代入反比例函数的表达式,即可求出答案;
(2)求出∠A=60°,∠B=30°,求出线段OA和OB,求出△AOB的面积,根据已知S△AOP![]() S△AOB,求出OP长,即可求出答案.
S△AOB,求出OP长,即可求出答案.
(1)把A(![]() ,1)代入反比例函数y
,1)代入反比例函数y![]() 得:k=1
得:k=1![]() ,所以反比例函数的表达式为y
,所以反比例函数的表达式为y![]() ;
;
(2)∵A(![]() ,1),OA⊥AB,AB⊥x轴于C,∴OC
,1),OA⊥AB,AB⊥x轴于C,∴OC![]() ,AC=1,OA
,AC=1,OA![]() 2.
2.
∵tanA![]() ,∴∠A=60°.
,∴∠A=60°.
∵OA⊥OB,∴∠AOB=90°,∴∠B=30°,∴OB=2OC=2![]() ,∴S△AOB
,∴S△AOB![]() OAOB
OAOB![]() 2×2
2×2![]() .
.
∵S△AOP![]() S△AOB,∴
S△AOB,∴![]() OP×AC
OP×AC![]() .
.
∵AC=1,∴OP=2![]() ,∴点P的坐标为(﹣2
,∴点P的坐标为(﹣2![]() ,0)或(2
,0)或(2![]() ,0).
,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目