题目内容
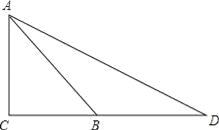
【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0），B（3，0）．
（1）求b、c．
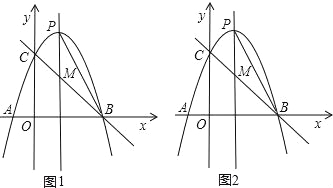
（2）如图1，在第一象限内的抛物线上是否存在点D，使得三角形BCD的面积最大？若存在，求出D点坐标，求出三角形BCD的面积最大值；若不存在，请说明理由．
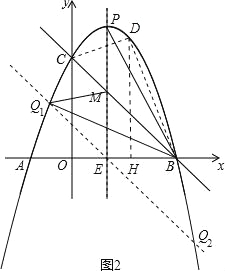
（3）如图2，抛物线的对称轴与抛物线交于点P，与直线BC相交于点M，连接PB．问在直线BC下方的抛物线上是否存在否存在点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】（1）y=-x2+2x+3；（2）（
，
），
；（3）Q1（
，
），Q2（
，-
）
【解析】
试题分析：（1）把A（-1，0）、B（3，0）两点代入y=-x2+bx+c，即可求出抛物线的解析式；
（2）设D点坐标为（t，-t2+2t+3），过点D作DH⊥x轴于H，根据
=-
t2+
t，再利用配方法即可求出D点坐标及△BCD面积的最大值；
（3）设PM与x轴交于点E，求出过点E与BC平行的直线EQ解析式为y=﹣x+1，解方程组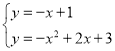
，即可得出点Q的坐标．
试题解析：（1）∵抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0），B（3，0），
∴
，
解得
，
∴抛物线的解析式为y=﹣x2+2x+3；
（2）如图1，设D点坐标为（t，﹣t2+2t+3），过点D作DH⊥x轴于H，
则
=
（﹣t2+2t+3+3）t+（3﹣t）（﹣t2+2t+3）﹣×3×3
=﹣t2+t
=﹣（t﹣）2+
，
∵﹣＜0，
∴当t=时，D点坐标是（，
），△BCD面积的最大值是
；
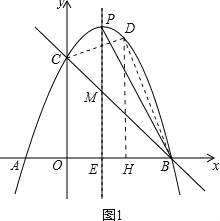
（3）如图2，设PM与x轴交于点E，
∵y=﹣x2+2x+3=﹣（x﹣1）2+4，
∴P点的坐标为（1，4），E点的坐标为（1，0）．
∵B（3，0），C（0，3），
∴直线BC的解析式为y=﹣x+3，
∴当x=1时，y=2，
∴M点的坐标为（1，2），
∴PM=ME=2，BM为△BPE的中线，
∴
．
过E作BC的平行线，交抛物线于点Q，则
，
∴
．
∵E（1，0），直线BC的解析式为y=﹣x+3，EQ∥BC，
∴直线EQ的解析式为y=﹣x+1．
由，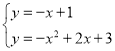
解得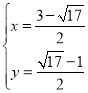
，或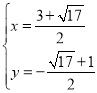
，
∴点Q的坐标为Q1（
，
），Q2（
，﹣
），
∴在直线BC下方的抛物线上存在点Q，使得△QMB与△PMB的面积相等，此时点Q的坐标为Q1（，），Q2（，﹣）．
