题目内容
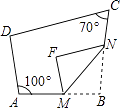
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度? 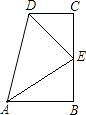
【答案】解:过点E作AD的垂线,垂足为F,∵∠DFE=∠C=90°,DE平分∠ADC,DE=DE,
∴△DCE≌△DFE(AAS),
∴∠DEC=∠DEF,EC=EF,
又∵EC=EB,则EF=EB,且∠B=∠EFA=90°,AE=AE,
∴△AFE≌△ABE(HL),
∴∠FEA=∠BEA,
又∵∠DEC+∠DEF+∠FEA+∠BEA=180°,
∴∠AED=90°,
∴∠CED+∠BEA=90°,
又∠EAB+∠BEA=90°,
∴∠EAB=∠CED=35°.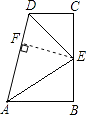
【解析】过点E作AD的垂线,垂足为F,根据∠DFE=∠C=90°,DE平分∠ADC,可证△DCE≌△DFE,可得∠DEC=∠DEF,EC=EF,又已知EC=EB,可得EF=EB,且∠B=∠EFA=90°,可证△AFE≌△ABE,可知∠FEA=∠BEA,又∠DEC+∠DEF+∠FEA+∠BEA=180°,从而可得∠AED=90°再利用互余关系证明∠EAB=∠CED.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和角平分线的性质定理的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
相关题目