题目内容
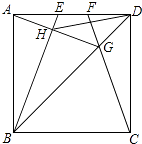
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
【答案】
(1)解:∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD= ![]() ,
,
∴AB=1,
∴正方形ABCD的边长为1;
(2)解:CN=2EM
证明方法一、理由:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC
∵CF=CA,CE是∠ACF的平分线,
∴CE⊥AF,AE=FE
∴EO为△AFC的中位线
∴EO∥BC
∴ ![]()
∴在Rt△AEN中,OA=OC
∴EO=OC= ![]() AC,
AC,
![]()
∴CM= ![]() EM
EM
∵CE平分∠ACF,
∴∠OCM=∠BCN,
∵∠NBC=∠COM=90°,
∴△CBN∽△COM,
∴ ![]() ,
,
∴CN= ![]() CM,
CM,
即CN=2EM.
证明方法二、∵四边形ABCD是正方形,
∴∠BAC=45°=∠DBC,
由(1)知,在Rt△ACE中,EO= ![]() AC=CO,
AC=CO,
∴∠OEC=∠OCE,
∵CE平分∠ACF,
∴∠OCE=∠ECB=∠OEC,
∴EO∥BC,
∴∠EOM=∠DBC=45°,
∵∠OEM=∠OCE
∴△EOM∽△CAN,
∴ ![]() ,
,
∴CN=2CM.
【解析】本题主要考查了相似三角形的判定和性质、三角形中位线、正方形的性质等,利用比例式判断出CM=![]() EM和CN=
EM和CN=![]() CM是解题的关键.
CM是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目