Question

【题目】如图，直角梯形纸片ABCD中，AD∥BC，∠A=90°，∠C=30°，折叠纸片使BC经过点D，点C落在点E处，BF是折痕，且BF=CF=8．

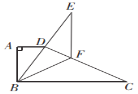
（1）求∠BDF的度数

（2）求AB的长．

Answer 1

【答案】（1）90°；（2）6.

【解析】

试题分析：（1）利用等边对等角可以得到∠FBC=∠C=30°，再利用折叠的性质可以得到∠EBF=∠CBF=30°，从而可以求得所求角的度数．

（2）利用上题得到的结论可以求得线段BD，然后在直角三角形ABD中求得AB即可．

试题解析：（1）∵BF=CF=8，

∴∠FBC=∠C=30°，

∵折叠纸片使BC经过点D，点C落在点E处，BF是折痕，

∴∠EBF=∠CBF=30°，

∴∠EBC=60°，

∴∠BDF=90°；

（2）∵∠EBC=60°

∴∠ADB=60°，

∵BF=CF=8．

∴BD=BF×sin60°=4

∴在Rt△BAD中，

AB=BD×sin60°=6．