题目内容
探索问题:(1)比较下列数的大小: ______
______ ,
,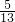 ______
______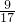 ,
,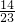 ______
______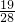 .
.
(2)根据上述规律,可以得出下面的结论:一个真分数 (a、b均为正数),给其分子、分母同加上一个正数m,得
(a、b均为正数),给其分子、分母同加上一个正数m,得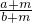 ,则这两个分数的大小关系是:
,则这两个分数的大小关系是: ______
______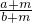 .
.
(3)请你用文字叙述(2)中的结论:______;
(4)请你用图形的面积说明(2)中结论的正确性.
(5)请你用已学的其他数学知识说明(2)中结论的正确性.
(6)这个结论可以解释生活中的许多现象,解决生活中许多与数学有关的问题.请你再提出一个类似的数学问题,或举出一个生活中与此结论相关的例子.
解:(1)通过分母通分得到分母相同的分式,然后比较分子大小得出结果.
∴ ,
, ,
,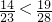 ;
;
(2)有第一问的结果可得出规律:分子分母同时加上一个正数比值变大.
所以: <
<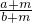 ;
;
(3)两正数的比值小于他们同时加上一个正数的比值;
(4)如图
矩形BEFG和矩形ABCD,
∵a<b,
∴am<bm,
∴am+ab<bm+ab,
即a(m+b)<b(m+a),
∴ <
<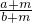 ;
;
(5)将两分式统分得分母为b(b+m),分子分别为a(b+m),
b(a+m)分子相减得(a-b)m,
由于 是真分式,
是真分式,
则a<b,
所以(a-b)m小于0,即 <
<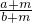 ;
;
(6)一杯糖水共b克,里面含有a克糖,糖的浓度为 ,然后往里放m克糖,
,然后往里放m克糖,
糖的浓度为: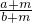 ,
,
放入糖后糖水变的更甜了,
所以加入糖后糖的浓度变大了,
所以 .
.
分析:(1)对于第一问的分式大小比较,通过通分比较大小;
(2)根据第一问的解找出规律: <
<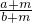 求解第二问;
求解第二问;
(3)用文字描述第二问得到的规律,两正数的比值小于他们同时加上一个正数的比值;
(4)分别以a,b为边长作矩形,又延长a,b同样长m,得三矩形面积分别为:ab,am,bm,然后根据长方形的面积比较两数大小;
(5)利用通分比较两式的大小;
(6)利用生活中的糖水的浓度问题来比较两式大小.
点评:此题是一个开放性试题,对于学生的要求比较高,首先根据第一问得出规律,然后用不同的方法证明次推论的正确性.本题意在考查用不同的方式比较两分式的大小,考查学生的发散思维.
∴
 ,
, ,
,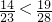 ;
;(2)有第一问的结果可得出规律:分子分母同时加上一个正数比值变大.
所以:
 <
<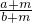 ;
;(3)两正数的比值小于他们同时加上一个正数的比值;
(4)如图

矩形BEFG和矩形ABCD,
∵a<b,
∴am<bm,
∴am+ab<bm+ab,
即a(m+b)<b(m+a),
∴
 <
<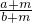 ;
;(5)将两分式统分得分母为b(b+m),分子分别为a(b+m),
b(a+m)分子相减得(a-b)m,
由于
 是真分式,
是真分式,则a<b,
所以(a-b)m小于0,即
 <
<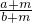 ;
;(6)一杯糖水共b克,里面含有a克糖,糖的浓度为
 ,然后往里放m克糖,
,然后往里放m克糖,糖的浓度为:
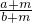 ,
,放入糖后糖水变的更甜了,
所以加入糖后糖的浓度变大了,
所以
 .
.分析:(1)对于第一问的分式大小比较,通过通分比较大小;
(2)根据第一问的解找出规律:
 <
<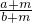 求解第二问;
求解第二问;(3)用文字描述第二问得到的规律,两正数的比值小于他们同时加上一个正数的比值;
(4)分别以a,b为边长作矩形,又延长a,b同样长m,得三矩形面积分别为:ab,am,bm,然后根据长方形的面积比较两数大小;
(5)利用通分比较两式的大小;
(6)利用生活中的糖水的浓度问题来比较两式大小.
点评:此题是一个开放性试题,对于学生的要求比较高,首先根据第一问得出规律,然后用不同的方法证明次推论的正确性.本题意在考查用不同的方式比较两分式的大小,考查学生的发散思维.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
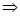
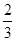
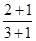 , ②
, ② , ③
, ③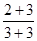 , ④
, ④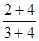 ,…。
,…。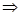
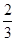
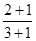 , ②
, ②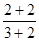 , ③
, ③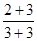 , ④
, ④ ,…。
,…。