题目内容

如图，已知抛物线y＝ax2－4x＋c经过点A(0，－6)和B(3，－9)，

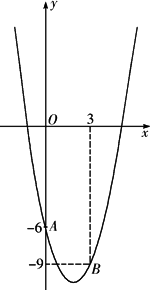
(1)求出抛物线的解析式；

(2)写出抛物线的对称轴方程及顶点坐标；

(3)点P(m，m)与点Q均在抛物线上(其中m＞0)，且这两点关于抛物线的对称轴，对称，求m的值及点Q的坐标；

(4)在满足(3)的情况下，在抛物线的对称轴上寻找一点M，使得△QMA的周长最小．

答案：
解析：

　　解：(1)依题意有．

　　即　　2分．

　　　　4分．

　　∴抛物线的解析式为：　　5分．

　　(2)把配方得，．

　　∴对称轴方程为　　7分．

　　顶点坐标　　10分．

　　(3)由点在抛物线上．

　　有　　12分．

　　即．

　　∴．

　　或(舍去)　　13分．

　　∴．

　　∵点、均在抛物线上，且关于对称轴对称．

　　∴　　15分．

　　(4)连接，直线与对称轴相交于点．

　　由于两点关于对称轴对称，由轴对称性质可知，此时的交点，能够使．

　　得△的周长最小　　17分．

　　设直线的解析式．

　　∴有．

　　∴．

　　∴直线的解析式为：　　18分．

　　设点．

　　则有　　19分．

　　此时点能够使得△的周长最小　　20分


练习册系列答案
相关题目

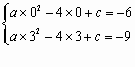如图，已知抛物线ｙ＝ｘ－ａｘ＋ａ－4ａ－4与ｘ轴相交于点A和点B，与ｙ轴相交于点D（0，8），直线DC平行于ｘ轴，交抛物线于另一点C，动点P以每秒2个单位长度的速度从C点出发，沿C→D运动，同时，点Q以每秒1个单位长度的速度从点A出发，沿A→B运动，连接PQ、CB，设点P运动的时间为t秒．

（１）求ａ的值；

（２）当四边形ODPQ为矩形时，求这个矩形的面积；

（３）当四边形PQBC的面积等于14时，求t的值．

（４）当t为何值时，△PBQ是等腰三角形？
（9分）如图，已知抛物线y＝x2＋bx－3a过点A(1，0)，B(0，－3)，与x轴交于另一点C．

(1)求抛物线的解析式；
(2)若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，
求点P的坐标；
(3)在(2)的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形
为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由．

（本题9分）如图，已知抛物线y＝ax2＋bx＋3的图象与x轴交于A、B两点，与y轴交于点C，且点C、D是抛物线上的一对对称点．

【小题1】(1)求抛物线的解析式；
【小题2】(2)求点D的坐标，并在图中画出直线BD；
【小题3】(3)求出直线BD的一次函数解析式，并根据图象回答：当x满足什么条件时，上述二次函数的值大于该一次函数的值．

（9分）如图，已知抛物线y＝x2＋bx－3a过点A(1，0)，B(0，－3)，与x轴交于另一点C．

(1)求抛物线的解析式；
(2)若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，
求点P的坐标；
(3)在(2)的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形
为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由．

（本题满分10分）

如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为x＝1，且抛物线经过A（—1，0）、C（0，—3）两点，与x轴交于另一点B．

1.（1）求这条抛物线所对应的函数关系式；

2.（2）在抛物线的对称轴x＝1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标；

3.（3）设点P为抛物线的对称轴x＝1上的一动点，求使∠PCB＝90°的点P的坐标．

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网