题目内容
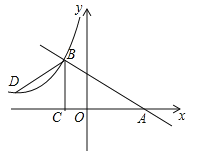
【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 . 
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
【答案】
(1)6;90°
(2)解:∵A1B1=AB=6,OA1﹣OA=6,∠OA1B1=∠OAB=90°,∠AOA1=90°,
∴∠OA1B1=∠AOA1,A1B1=OA,
∴B1A1∥OA,
∴四边形OAA1B1是平行四边形
(3)解:S=OAA1O=6×6=36.
即四边形OAA1B1的面积是36
【解析】解:(1)A1B1=AB=6,∠AOA1=90°.
故答案是:6,90°;
【考点精析】本题主要考查了平行四边形的判定和旋转的性质的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
相关题目