Question

【题目】图①为平地上一幢建筑物与铁塔图，图②为其示意图．建筑物AB与铁塔CD都垂直于地面，BD=20m，在A点测得D点的俯角为45°，测得C点的仰角为58°．求铁塔CD的高度．（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）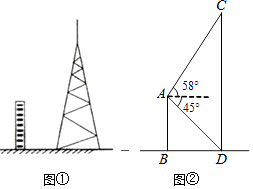

Answer 1

【答案】解：如图，过点A作AE⊥CD，垂足为E，

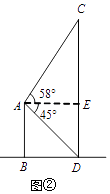
则四边形ABDE矩形，

∵BD=20m，在A点测得D点的俯角为45°，在测得C点的仰角为58°，

∴∠ADB=∠EAD=45°，

∴AB=ED=BD=20m，

在Rt△AEC中，tan∠CAE= ，

∴tan58°= = ，

∴CE=20 tan58°=20×1.60=32，

∴CD=CE+ED=32+20=52米．

答：铁塔CD的高度为52米．

【解析】先过点A作AE⊥CD，垂足为E，则四边形ABDE矩形，根据∠ADB=∠EAD=45°，可得AB=ED=BD=20m，在Rt△AEC中，根据正切定义得出tan∠CAE,求得CE的长，进而得到铁塔CD的高度．

【考点精析】掌握关于仰角俯角问题是解答本题的根本，需要知道仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．