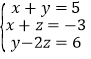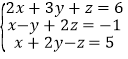题目内容
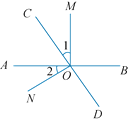
【题目】如图，直线AB，CD相交于点O，过点O作两条射线OM，ON，且∠AOM＝∠CON＝90°.
(1)若OC平分∠AOM，求∠AOD的度数；
(2)若∠1＝∠BOC，求∠AOC和∠MOD.
【答案】（1）135°（2）150°
【解析】
①根据角平分线定义求出∠1=∠AOC=45°，代入∠AOD=180°-∠AOC求出即可；
②求出∠BOM=180°-90°=90°，根据∠1=
∠BOC求出∠1=
∠BOM=30°，即可求出答案．
(1)因为∠AOM＝∠CON＝90°，OC平分∠AOM，所以∠1＝∠AOC＝45°，所以∠AOD＝180°－∠AOC＝180°－45°＝135°.
(2)因为∠AOM＝90°，所以∠BOM＝180°－90°＝90°.因为∠1＝∠BOC，所以∠1＝∠BOM＝30°，所以∠AOC＝90°－30°＝60°，∠MOD＝180°－30°＝150°.
练习册系列答案
相关题目
【题目】深圳市某学校抽样调查，A类学生骑共享单车，B类学生坐公交车、私家车等，C类学生步行，D类学生（其它），根据调查结果绘制了不完整的统计图．
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
（1）学生共人， 
， 
；
（2）补全条形统计图；
（3）若该校共有2000人，骑共享单车的有人．
