题目内容
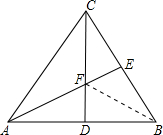
在等腰△ABC中,CD是底边AB上的高,E是腰BC的中点,AE与CD交于F,现给出三条路线:
(a)A→F→C→E→B→D→A;
(b)A→C→E→B→D→F→A;
(c)A→D→B→E→F→C→A;
它们的长度分别记为L(a)、L(b)及L(c),则L(a)<L(b),L(a)<L(c),L(b)<L(c)中一定能成立的是______.
(a)A→F→C→E→B→D→A;
(b)A→C→E→B→D→F→A;
(c)A→D→B→E→F→C→A;
它们的长度分别记为L(a)、L(b)及L(c),则L(a)<L(b),L(a)<L(c),L(b)<L(c)中一定能成立的是______.
依题意,知F是△ABC的重心.
∴CF=aDF,AF=a0F,AF=BF,
∵L(a)=AF+FC+CB+BA
L(c)=AB+B0+0F+FC+CA
∴L(c)-L(a)=(AB-BD)+(0F-FA)+(FC-DF)-C0=AD+DF-C0-0F
当△ABC为等边三角形时,AD=C0,DF=0F,此时有L(a)-L(b)=FC+DA-AC-DF=DF+DA-AC由于当∠ACB较大时,AC与AD可以很接近,取CD足够长可使L(a)>L(b),如取∠ACB=ba0°,AC=BC=b,则AD=
,CD=
DF=
∴L(a)-L(b)=
+
-b=
-b>0故L(a)<L(b)不恒成立.
故答案为L(a)<L(b).

∴CF=aDF,AF=a0F,AF=BF,
∵L(a)=AF+FC+CB+BA
L(c)=AB+B0+0F+FC+CA
∴L(c)-L(a)=(AB-BD)+(0F-FA)+(FC-DF)-C0=AD+DF-C0-0F
当△ABC为等边三角形时,AD=C0,DF=0F,此时有L(a)-L(b)=FC+DA-AC-DF=DF+DA-AC由于当∠ACB较大时,AC与AD可以很接近,取CD足够长可使L(a)>L(b),如取∠ACB=ba0°,AC=BC=b,则AD=
| ||
| a |
| b |
| a |
| b |
| 6 |
∴L(a)-L(b)=
| ||
| a |
| b |
| 6 |
3
| ||
| 6 |
故答案为L(a)<L(b).

练习册系列答案
相关题目

 的解集在数轴上表示为 ( )
的解集在数轴上表示为 ( )