题目内容
如图9,等边![]() 边长为4,
边长为4,![]() 是边
是边![]() 上动点,
上动点,![]() 于H,过
于H,过![]() 作
作![]() ∥
∥![]() ,交线段
,交线段![]() 于点
于点![]() ,在线段
,在线段![]() 上取点
上取点![]() ,使
,使![]() .设
.设![]() .
.
(1)请直接写出图中与线段![]() 相等的两条线段(不再另外添加辅助线);
相等的两条线段(不再另外添加辅助线);
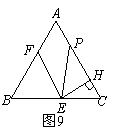 (2)
(2)![]() 是线段
是线段![]() 上的动点,当四边形
上的动点,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的面积(用含
的面积(用含![]() 的代数式表示)
的代数式表示)![]() ;
;
(3)当(2)中 的![]() 面积最大时,以E为圆心,
面积最大时,以E为圆心,![]() 为半径作圆,根据⊙E与此时
为半径作圆,根据⊙E与此时![]() 四条边交点的总个数,求相应
四条边交点的总个数,求相应![]() 的取值范围.
的取值范围.
解:(1)BE、PE、BF三条线段中任选两条.………………………2分
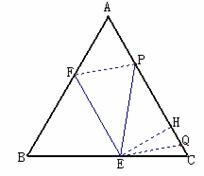 (2)在Rt△CHE中,∠CHE=90° ∠C=60°,
(2)在Rt△CHE中,∠CHE=90° ∠C=60°,
∴EH=![]()
∵PQ=EF=BE=4-x
∴![]() .……………………5分
.……………………5分
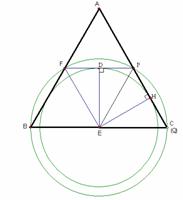 (3)
(3)
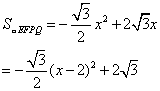
∴当x=2时,![]() 有最大值.
有最大值.
此时E、F、P分别为△ABC三边BC、AB、AC的中点,且点C、 点Q重合
∴平行四边形EFPQ是菱形.
过E点作ED⊥FP于D,
∴ED=EH=![]() .
.
∴当⊙E与□EFPQ四条边交点的总个数是2个时,0<r<![]() ;
;
当⊙E与□EFPQ四条边交点的总个数是4个时,r=![]() ;
;
当⊙E与□EFPQ四条边交点的总个数是6个时,![]() <r<2;
<r<2;
当⊙E与□EFPQ四条边交点的总个数是3个时,r=2时;
当⊙E与□EFPQ四条边交点的总个数是0个时,r>2时.
…………………………………………………………12分
易错分析:本题在分类中,容易把⊙E与□EFPQ四条边交点的总个数分不清楚,容易出现交点数多或少的漏洞.

练习册系列答案
相关题目
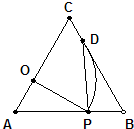 18、如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于点D,连接PD,如果PO=PD,那么AP的长是( )
18、如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于点D,连接PD,如果PO=PD,那么AP的长是( ) 如图,在等边△ABC中,AC=9,点O在AC上,且A0=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于点D,连接PD,如果PO=PD,那么AP的长是
如图,在等边△ABC中,AC=9,点O在AC上,且A0=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于点D,连接PD,如果PO=PD,那么AP的长是
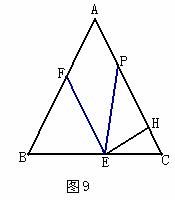 如图9,等边
如图9,等边