题目内容
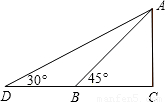
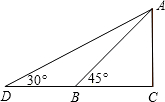 某风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,如图,改善后的台阶坡面AD的长为50m(BC所在地面为水平面),坡角由45°减至30°.
某风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,如图,改善后的台阶坡面AD的长为50m(BC所在地面为水平面),坡角由45°减至30°.(1)求改善前的台阶坡面AB的长;
(2)求台阶所在地面增加部分BD的长.(计算结果都保留根号).
分析:(1)根据题义求出AC,再在Rt△ACB中求得AB.
(2)在Rt△ACD中利用三角函数求得DC,再在Rt△ACB中,求出BC即可得出BD.
(2)在Rt△ACD中利用三角函数求得DC,再在Rt△ACB中,求出BC即可得出BD.
解答:解:(1)在Rt△ACD中∠D=30°,AD=50,(1分)
∵sin∠D=
,
∴AC=AD•sin∠D,(2分)
=50×
=25,
在Rt△ACB中∠ABC=45°,(3分)
∵sin∠ACB=
,
∴AB=
,(4分)
=
=25
,
答:改善前的台阶坡面AB的长为25
米.
(2)在Rt△ACD中∠D=30°,AD=50,
∵cos∠D=
,
∴DC=AD•cos∠D,(6分)
=50×
=25
,
又∵在Rt△ACB中∠ABC=45°,
∴∠BAC=∠ABC=45°,(7分)
∴BC=AC=25,(8分)
∴BD=DC-BC=25
-25.(9分)
答:台阶所在地面增加部分BD的长为(25
-25)米.
∵sin∠D=
| AC |
| AD |
∴AC=AD•sin∠D,(2分)
=50×
| 1 |
| 2 |
在Rt△ACB中∠ABC=45°,(3分)
∵sin∠ACB=
| AC |
| AB |
∴AB=
| AC |
| sin∠ABC |
=
| 25 | ||||
|
| 2 |
答:改善前的台阶坡面AB的长为25
| 2 |
(2)在Rt△ACD中∠D=30°,AD=50,
∵cos∠D=
| DC |
| AD |
∴DC=AD•cos∠D,(6分)
=50×
| ||
| 2 |
| 3 |
又∵在Rt△ACB中∠ABC=45°,
∴∠BAC=∠ABC=45°,(7分)
∴BC=AC=25,(8分)
∴BD=DC-BC=25
| 3 |
答:台阶所在地面增加部分BD的长为(25
| 3 |
点评:本题是基础题,考查了解直角三角形的应用坡度坡角问题,以及勾股定理的运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).
把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).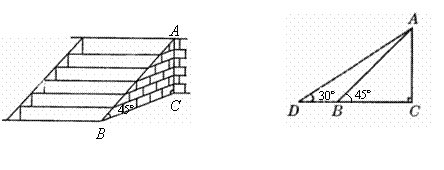 (2)改善后的台阶多占多长一段水平地面?(结果精确到
(2)改善后的台阶多占多长一段水平地面?(结果精确到