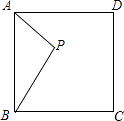
题目内容
【题目】在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S2+S3+S4= 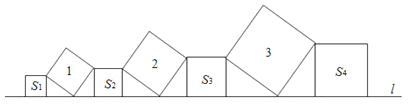
【答案】4
【解析】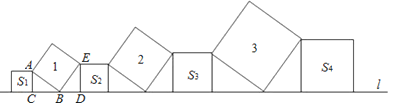
解:观察发现,
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD,
∴△ABC≌△BDE(AAS),
∴BC=ED,
∵AB2=AC2+BC2 ,
∴AB2=AC2+ED2=S1+S2 ,
即S1+S2=1,
同理S3+S4=3.
则S1+S2+S3+S4=1+3=4.
故答案为:4.
运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.

练习册系列答案
相关题目