题目内容
【题目】P为正方形ABCD内一点,且AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D. 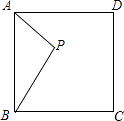
(1)作出旋转后的图形;
(2)试求△APP′的周长和面积.
【答案】
(1)解:如图所示:△AP′D即为所求;
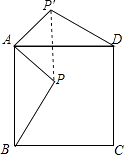
(2)解:∵AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D,
∴AP′=AP=2,∠PAP′=90°,
∴PP′=2 ![]() ,
,
故△APP′的周长为:2+2+2 ![]() =4+2
=4+2 ![]() ;
;
△APP′的面积为: ![]() ×2×2=2.
×2×2=2.
【解析】(1)利用题意得出对应点P′的位置进而得出答案;(2)利用等腰直角三角形的性质求出周长和面积即可.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目