题目内容
已知:如图,∠EAC是⊿ABC的外角,AD平分∠EAC,且AD∥BC,
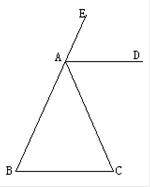
求证:AB=AC

求证:AB=AC
见解析
证明:∵AD∥BC
∴∠EAD =∠B,∠DAC =∠C
∵AD平分∠EAC
∴∠EAD=∠DAC,
∴∠B=∠C
∴AB=AC
先根据平行线性质得到∠EAD=∠B,∠DAC=∠C,再根据角平分线的性质得到∠EAD=∠DAC,从而推出∠B=∠C,等角对等边所以AB=AC.
∴∠EAD =∠B,∠DAC =∠C
∵AD平分∠EAC
∴∠EAD=∠DAC,
∴∠B=∠C
∴AB=AC
先根据平行线性质得到∠EAD=∠B,∠DAC=∠C,再根据角平分线的性质得到∠EAD=∠DAC,从而推出∠B=∠C,等角对等边所以AB=AC.

练习册系列答案
相关题目



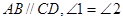 求证:
求证: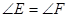
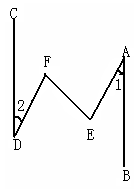

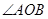 ,利用尺规作
,利用尺规作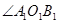 ,使得
,使得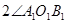 (要求不写做法,但要保留做图痕迹)(6分)(4分)
(要求不写做法,但要保留做图痕迹)(6分)(4分)