题目内容
我们容易发现:反比例函数的图象是一个中心对称图形,你可以利用这一结论解决问题。
如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形,若它与反比例函数 的图象分别交于第一、三象限的点B,D,已知点A(-m,0)、C(m,0)。
的图象分别交于第一、三象限的点B,D,已知点A(-m,0)、C(m,0)。
(1)直接判断并填写:不论α取何值,四边形ABCD的形状一定是_______;
(2)①当点B为(p,1)时,四边形ABCD是矩形,试求p,α,和m的值;
②观察猜想:对①中的m值,能使四边形ABCD为矩形的点B共有几个?(不必说理)
(3)试探究:四边形ABCD能不能是菱形?若能,直接写出B点的坐标,若不能,说明理由。
如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形,若它与反比例函数
 的图象分别交于第一、三象限的点B,D,已知点A(-m,0)、C(m,0)。
的图象分别交于第一、三象限的点B,D,已知点A(-m,0)、C(m,0)。(1)直接判断并填写:不论α取何值,四边形ABCD的形状一定是_______;
(2)①当点B为(p,1)时,四边形ABCD是矩形,试求p,α,和m的值;
②观察猜想:对①中的m值,能使四边形ABCD为矩形的点B共有几个?(不必说理)
(3)试探究:四边形ABCD能不能是菱形?若能,直接写出B点的坐标,若不能,说明理由。

| 解:(1)平行四边形; | |
(2)①∵点B(p,1)在 的图象上, 的图象上,∴  ∴  , ,过B作BE⊥x轴于E,则  ,BE=1, ,BE=1,在Rt△BOE中,  ,α=30°, ,α=30°,∴OB=2, 又∵点B、D是正比例函数与反比例函数图象的交点, ∴点B、D关于原点O成中心对称, ∴OB=OD=, ∵四边形ABCD为矩形,且A(-m,0),C(m,0) ∴  , ,∴m=2; ②能使四边形为ABCD矩形的点B共有2个; |
 |
| (3)四边形ABCD不能是菱形, ∵点A、C的坐标分别为(-m,0)、(m,0) ∴四边形ABCD的对角线AB在x轴上, 又∵点B、D分别是正比例函数与反比例函数在第一、三象限的交点, ∴对角线AC与BD不可能垂直, ∴四边形ABCD不能是菱形。 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
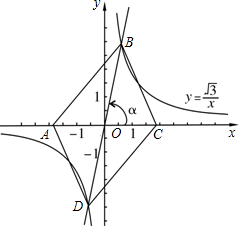 我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数
我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数 我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数
我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数 度后的图形。它与反比例函数
度后的图形。它与反比例函数 的图象分别交于第一、三象限的点B、D,已知点A(-m,0)、C(m,0)。
的图象分别交于第一、三象限的点B、D,已知点A(-m,0)、C(m,0)。
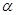 度后的图形。它与反比例函数
度后的图形。它与反比例函数 的图象分别交于第一、三象限的点B、D,已知点A(-m,0)、C(m,0)。
的图象分别交于第一、三象限的点B、D,已知点A(-m,0)、C(m,0)。