题目内容
设x、y是有理数，并且x、y满足等式x2+2y+
y=17-4，求x+y的值．
解：∵x、y为有理数，
∴x2+2y为有理数，
又∵x2+2y+y=17-4
∴
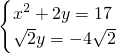
∴y=-4，x=±5
当x=+5时，x+y=-4+5=1
当x=-5时，x+y=-4-5=-9．
分析：因为x、y为有理数，所以x2+2y也是有理数，根据二次根式的性质，只有同类二次根式才能合并，所以x2、2y都不能与进行合并．又因为等式的右边有-4，所以y只能等于-4，x2+2y=17，把y=-4代入x2+2y=17中，得x2=25，x=±5．
点评：两个有理数的和一定是有理数，因此此题中y≠0．
∴x2+2y为有理数，
又∵x2+2y+
y=17-4∴
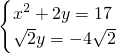
∴y=-4，x=±5
当x=+5时，x+y=-4+5=1
当x=-5时，x+y=-4-5=-9．
分析：因为x、y为有理数，所以x2+2y也是有理数，根据二次根式的性质，只有同类二次根式才能合并，所以x2、2y都不能与
进行合并．又因为等式的右边有-4，所以y只能等于-4，x2+2y=17，把y=-4代入x2+2y=17中，得x2=25，x=±5．点评：两个有理数的和一定是有理数，因此此题中
y≠0． 
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
、－a、
三数的点的大致位置，并简述理由．然后据此将上述5个有理数按从小到大的顺序排列，用小于号连接起来．
+
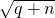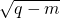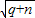，则p（________）．
+
，则p（______）．