Question

已知：m，n是两个连续自然数（m＜n），且q=mn．设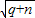p=+，则p（______）．
A、总是奇数；B、总是偶数；C、有时是奇数，有时是偶数；D、有时是有理数，有时是无理数．
请选出答案，并给出证明过程．

Answer 1

【答案】分析：根据已知条件可知n=m+1，代入所求代数式即可得出2p=m+1，故p为奇数．
解答：解：选A；
证明：由已知得n=m+1，
则q=mn=m（m+1），q+n=m（m+1）+（m+1）=m²+m+m+1=m²+2m+1=（m+1）²
q-m=m（m+1）-m=m²，
∴p=+=m+1+m=2m+1，
所以p为奇数．
点评：解答此题的关键是熟知自然数、奇数、偶数的定义，会进行整式的变形．