题目内容
综合与探究
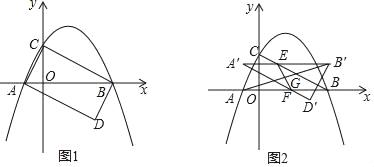
如图1,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C,连接AC,BC.D为坐标平面第四象限内一点,且使得△ABD与△ABC全等.
(1)求抛物线的表达式.
(2)请直接写出点D的坐标,并判断四边形ACBD的形状.
(3)如图2,将△ABD沿y轴的正方形以每秒1个单位长度的速度平移,得到△A′B′D′,A′B′与BC交于点E,A′D′与AB交于点F.连接EF,AB′,EF与AB′交于点G.设运动的时间为t(0≤t≤2)秒.
①当直线EF经过抛物线的顶点T时,请求出此时t的值;
②请直接写出点G经过的路径的长.
练习册系列答案
相关题目
如图1,点O是矩形ABCD的中心(对角线的交点),AB=4cm,AD=6cm.点M是边AB上的一动点,过点O作ON⊥OM,交BC于点N,设AM=x,ON=y,今天我们将根据学习函数的经验,研究函数值y随自变量x的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量x的取值范围是______;
(2)通过计算,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 2.40 | 2.24 | 2.11 | 2.03 | __ | __ | 2.11 | 2.24 | 2.40 |
请你补全表格(说明:补全表格时相关数值保留两位小数,参考数据: ≈3.04,
≈3.04,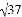 ≈6.09)
≈6.09)
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象.
(4)根据图象,请写出该函数的一条性质.



 ,得到△COD,则CD的长度是( )
,得到△COD,则CD的长度是( )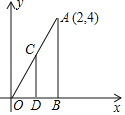
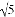
 (m是常数),当m取何值时,y随x的增大而减小( )
(m是常数),当m取何值时,y随x的增大而减小( ) x2-x+1=__________.
x2-x+1=__________.