题目内容
已知∠MAN=120°,AC平分∠MAN.
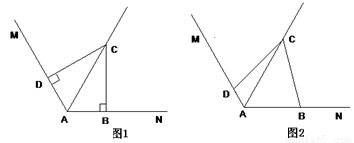
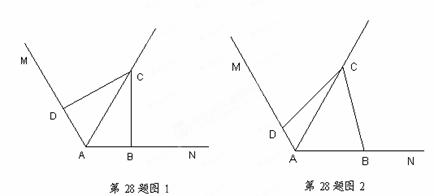
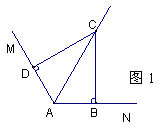
(1)在图1中,∠ABC=∠ADC=90°,则能得如下两个结论:
① DC = BC; ②AD+AB=AC.请你证明结![]() 论②;
论②;
(2)在图2中,若条件改为∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
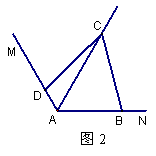 | |||
 | |||
(1)证明:∵∠MAN=120°,AC平分∠MAN
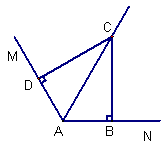 ∴∠MAC=∠NAC=60° ∠ACD=30°
∴∠MAC=∠NAC=60° ∠ACD=30°
又∵∠ABC=∠ADC=90° AC=AC
∴⊿ACD≌⊿ACB (AAS)
∴ AD=AB=![]() AC ∴AD+AB=AC
AC ∴AD+AB=AC
(2) 仍然成立 …1分
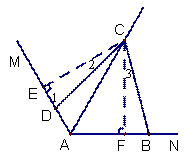 过C作CE⊥AM于E,作CF⊥AB于F
过C作CE⊥AM于E,作CF⊥AB于F
由(1)的证明结论,得到:
CE=CF AE+AF=AC …2分
∵∠ABC+∠ADC=180° ∠ADC+∠1=180°
∴∠1=∠ABC …3分
又∵∠ABC+∠ADC=180° ∠MAN=120°
∴ ∠DCB=60°
又∵∠AEC=∠AFC=90° ∠MAN=120°
∴∠ECF=60° ∴∠ECF=∠DCB=60° …5分
∴∠2=∠3 又∵∠AEC=∠BFC=90° CE=CF
∴⊿CED≌⊿CFB (ASA)
∴DE=BF CD=CB
∴AD+AB=AD+BF+AF=AD+DE+AF=AE+AF=AC …8分

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目