Question

【题目】（1）探索：请你利用图（1）验证勾股定理．

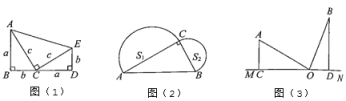
（2）应用：如图（2），已知在中，，，分别以AC，BC为直径作半圆，半圆的面积分别记为，，则______.（请直接写出结果）．

（3）拓展：如图（3），MN表示一条铁路，A，B是两个城市，它们到铁路所在直线MN的垂直距离分别为千米，千米，且千米．现要在CD之间建一个中转站O，求O应建在离C点多少千米处，才能使它到A，B两个城市的距离相等．

Answer 1

【答案】（1）见解析；（2）；（3）O应建在离C点52.5千米处．

【解析】

（1）此直角梯形的面积由三部分组成，利用直角梯形的面积等于三个直角三角形的面积之和列出方程并整理即可；
（2）根据半圆面积公式以及勾股定理，知S1+S2等于以斜边为直径的半圆面积；
（3）设CO=xkm，则OD=（80-x）km，在Rt△AOC和Rt△BOD中，利用勾股定理分别表示出AO和BO的长，根据AO=BO列出方程，求解即可．

（1）由面积相等可得，

∴，

∴，

∴．

（2），，

∴．

故答案为：

（3）设千米，则千米．

∵到A，B两个城市的距离相等，

∴，即，

由勾股定理，得，

解得．

即O应建在离C点52.5千米处．