题目内容
【题目】如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF. 
(1)求证:△DAC≌△ECP;
(2)填空: ①四边形ACED是何种特殊的四边形?
②在点P运动过程中,线段DF、AP的数量关系是 ![]() .
.
【答案】
(1)证明:∵DE为切线,
∴OD⊥DE,
∴∠CDE=90°,
∵点C为AP的中点,
∴DC⊥AP,
∴∠DCA=∠DCP=90°,
∵AB是⊙O直径,
∴∠APB=90°,
∴四边形DEPC为矩形,
∴DC=EP,
在△DAC和△ECP中
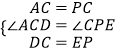 ,
,
∴△DAC≌△ECP;
(2)①∵△DAC≌△ECP,
∴AD=CE,∠DAC=∠ECP,
∴AD∥CE,
∴四边形ACED是平行四边形
②线段DF、AP的数量关系是DF= ![]() AP
AP
【解析】②∵OA=OD, ∴∠DAO=∠ADO,
∵AD∥CE,
∴∠ADO=∠DCF,
∴∠DAO=∠DCF,
∴A,C,F,D四点共圆,
∴ ![]() =
= ![]() ,
,
∴AC=DF,
∵AC= ![]() AP,
AP,
∴DF= ![]() AP,
AP,
所以答案是:DF= ![]() AP.
AP.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某中学七年级四班的同学在体检中测量了自己的身高,并求出了该班同学的平均身高.
(1)下表给出了该班5名同学的身高情况(单位:cm),试完成该表,并求出该班同学的平均身高.
姓名 | 刘杰 | 刘涛 | 李明 | 张春 | 刘建 |
身高 | 161 |
|
| 165 | 155 |
身高与全班同 学平均身高差 | +3 | ﹣1 | 0 |
|
|
(2)谁最高?谁最矮?
(3)计算这5名同学的平均身高是多少?