题目内容
l1、l2表示直线，给出下列四个论断：①l1∥l2；②l1切⊙O于点A；③l2切⊙O于点B；④AB是⊙O的直径．若以其中三个论断作为条件，余下的一个作为结论，可以构造出一些命题，在这些命题中，正确命题的个数为
- A.1
- B.2
- C.3
- D.4
D
分析：根据直线与圆的位置关系、平行线的性质定理来分析判断．分以下四种情况讨论：
第一种情况：①②③?④；第二种情况：①②④?③；第三种情况：①③④?②；第四种情况：②③④?①．
解答：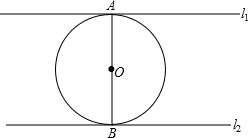
解：第一种情况：①②③?④
∵l1切⊙O于点A，l2切⊙O于点B
∴OA⊥l1，OB⊥l2
又∵l1∥l2
∴OA⊥l2
∴OA、OB为在同一条上
∴AB是⊙O的直径
命题成立；
第二种情况：①②④?③
∵l1切⊙O于点A
∴OA⊥l1，
∵AB是⊙O的直径；l1∥l2
∴AB⊥l2
即l2切⊙O于点B
命题成立；
第三种情况：①③④?②
同第二种情况；
命题成立
第四种情况：②③④?①．
∵l1切⊙O于点A，l2切⊙O于点B
∴OA⊥l1，OB⊥l2
又∵AB是⊙O的直径
∴l1∥l2
命题成立．
故答案为D
点评：本题考查直线与圆的位置关系、平行线的性质．解决本题一定要分类讨论，并证明之．
分析：根据直线与圆的位置关系、平行线的性质定理来分析判断．分以下四种情况讨论：
第一种情况：①②③?④；第二种情况：①②④?③；第三种情况：①③④?②；第四种情况：②③④?①．
解答：
解：第一种情况：①②③?④∵l1切⊙O于点A，l2切⊙O于点B
∴OA⊥l1，OB⊥l2
又∵l1∥l2
∴OA⊥l2
∴OA、OB为在同一条上
∴AB是⊙O的直径
命题成立；
第二种情况：①②④?③
∵l1切⊙O于点A
∴OA⊥l1，
∵AB是⊙O的直径；l1∥l2
∴AB⊥l2
即l2切⊙O于点B
命题成立；
第三种情况：①③④?②
同第二种情况；
命题成立
第四种情况：②③④?①．
∵l1切⊙O于点A，l2切⊙O于点B
∴OA⊥l1，OB⊥l2
又∵AB是⊙O的直径
∴l1∥l2
命题成立．
故答案为D
点评：本题考查直线与圆的位置关系、平行线的性质．解决本题一定要分类讨论，并证明之．
练习册系列答案
相关题目
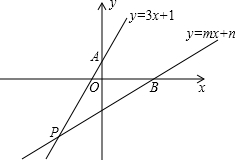如图，已知直线l1：y=3x+1与y轴交于点A，且和直线l2：y=mx+n交于点P（-2，a），根据以上信息解答下列问题：
（2011•裕华区二模）如图，直线l1与l2相交于点P，点P横坐标为-1，l1的解析表达式为y=