题目内容
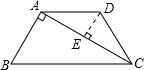
如图，在梯形ABCD中，AD∥BC，AC⊥AB，AD=CD，cosB=
，BC=26．
求：（1）cos∠DAC的值；
（2）线段AD的长．
| 5 |
| 13 |
求：（1）cos∠DAC的值；
（2）线段AD的长．
（1）在Rt△ABC中，∠BAC=90°，cosB=
=
．
∵BC=26，
∴AB=10．
∴AC=
=
=24．
∵AD∥BC，
∴∠DAC=∠ACB．
∴cos∠DAC=cos∠ACB=
=
．
（2）过点D作DE⊥AC，垂足为E，
∵AD=CD，AC=24，
∴AE=EC=
AC=12，又AD=DC，
∴在Rt△ADE中，cos∠DAE=
=
．
∴AD=13．
| AB |
| BC |
| 5 |
| 13 |
∵BC=26，
∴AB=10．
∴AC=
| BC2-AB2 |
| 262-102 |
∵AD∥BC，
∴∠DAC=∠ACB．
∴cos∠DAC=cos∠ACB=
| AC |
| BC |
| 12 |
| 13 |
（2）过点D作DE⊥AC，垂足为E，
∵AD=CD，AC=24，
∴AE=EC=
| 1 |
| 2 |
∴在Rt△ADE中，cos∠DAE=
| AE |
| AD |
| 12 |
| 13 |
∴AD=13．
练习册系列答案
相关题目
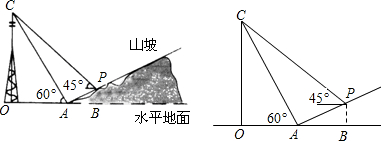
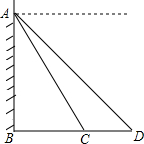
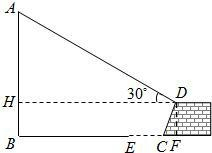时，为确保安全是否将此行车道封上？请说明理由．
为C，连接AC．