Question

【题目】如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB交BC于点D,OE∥AC交BC于点E.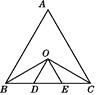

（1）试判断△ODE的形状,并说明你的理由;
（2）若BC=10,求△ODE的周长.

Answer 1

【答案】
（1）解：△ODE是等边三角形.理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.
∴∠DOE=60°.
∴∠DOE=∠ODE=∠OED.
∴△ODE是等边三角形 。
（2）解：∵BO平分∠ABC,且∠ABC=60°,
∴∠OBD=30°.
∴∠BOD=∠ODE-∠OBD=60°-30°=30°.
∴∠OBD=∠BOD.
∴BD=OD.
同理可得:CE=OE.
∴△ODE的周长=OD+DE+OE=BD+DE+CE=BC=10
【解析】（1）△ODE是等边三角形.理由如下:根据等边三角形的性质得出∠ABC=∠ACB=60°，根据二直线平行，同位角相等得出∠ODE=∠ABC=60°,∠OED=∠ACB=60°，根据三角形的内角和得出∠DOE=60°，从而得出∠DOE=∠ODE=∠OED，根据三个内角都相等的三角形是等边三角形得出△ODE是等边三角形；
（2）根据角平分线的定义得出∠OBD=30°，根据三角形的外角定理得出∠BOD=∠ODE-∠OBD=60°-30°=30°，从而得出∠OBD=∠BOD，根据等角对等边得出BD=OD，同理可得:CE=OE，根据△ODE的周长=OD+DE+OE=BD+DE+CE=BC得出结论。