题目内容
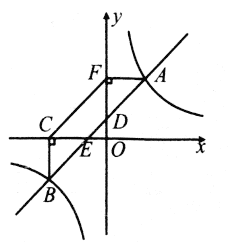
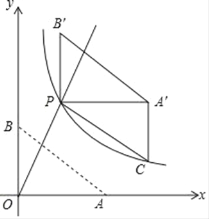
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
(1)求k1与k2的值;
(2)求直线PC的表达式;
(3)直接写出线段AB扫过的面积.
【答案】(1)k1=2,k2=8;(2)y=﹣![]() x+
x+![]() ;(3)22.
;(3)22.
【解析】
(1)把点P(2,4)代入直线y=k1x,把点P(2,4)代入双曲线y=![]() ,可得k1与k2的值;
,可得k1与k2的值;
(2)根据平移的性质,求得C(6,![]() ),再运用待定系数法,即可得到直线PC的表达式;
),再运用待定系数法,即可得到直线PC的表达式;
(3)延长A'C交x轴于D,过B'作B'E⊥y轴于E,根据△AOB≌△A'PB',可得线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积,据此可得线段AB扫过的面积.
(1)把点P(2,4)代入直线y=k1x,可得4=2k1,
∴k1=2,
把点P(2,4)代入双曲线y=![]() ,可得k2=2×4=8;
,可得k2=2×4=8;
(2)∵A(4,0),B(0,3),
∴AO=4,BO=3,
如图,延长A'C交x轴于D,
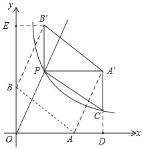
由平移可得,A'P=AO=4,
又∵A'C∥y轴,P(2,4),
∴点C的横坐标为2+4=6,
当x=6时,y=![]() ,即C(6,
,即C(6,![]() ),
),
设直线PC的解析式为y=kx+b,
把P(2,4),C(6,![]() )代入可得
)代入可得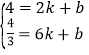 ,解得
,解得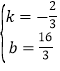 ,
,
∴直线PC的表达式为y=﹣![]() x+
x+![]() ;
;
(3)如图,延长A'C交x轴于D,
由平移可得,A'P∥AO,
又∵A'C∥y轴,P(2,4),
∴点A'的纵坐标为4,即A'D=4,
如图,过B'作B'E⊥y轴于E,
∵PB'∥y轴,P(2,4),
∴点B'的横坐标为2,即B'E=2,
又∵△AOB≌△A'PB',
∴线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积=BO×B'E+AO×A'D=3×2+4×4=22.