题目内容
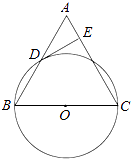
【题目】如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是等腰三角形时,求m的值;
(3)设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图2),当点P从点O向点C运动时,点H也随之运动.请直接写出点H所经过的路径长.(不必写解答过程)
【答案】
(1)
解:由题意得CM=BM,
∵∠PMC=∠DMB,
∴Rt△PMC≌Rt△DMB,
∴DB=PC,
∴DB=2﹣m,AD=4﹣m,
∴点D的坐标为(2,4﹣m)
(2)
解:分三种情况
①若AP=AD,则4+m2=(4﹣m)2,解得 ![]() ;
;
②若PD=PA
过P作PF⊥AB于点F(如图),
则AF=FD= ![]() AD=
AD= ![]() (4﹣m)
(4﹣m)
又∵OP=AF,
∴ ![]()
则 ![]()
③若PD=DA,
∵△PMC≌△DMB,
∴PM= ![]() PD=
PD= ![]() AD=
AD= ![]() (4﹣m),
(4﹣m),
∵PC2+CM2=PM2,
∴ ![]() ,
,
解得 ![]() (舍去).
(舍去).
综上所述,当△APD是等腰三角形时,m的值为 ![]() 或
或 ![]() 或
或 ![]()

(3)
解:点H所经过的路径长为 ![]() ;
;
理由是:∵P(0,m)是线段OC上一动点(C点除外),
∴0≤m<2,
当O与P重合时,P点才开始运动,过P、M、B三点的抛物线y=﹣x2+3x,
此时ME的解析式为y=﹣x+3,则∠MEO=45°,
又∵OH⊥EM,
∴△OHE为等腰直角三角形,
∴点O、H、B三点共线,
∴点H所经过的路径以OM为直径的劣弧 ![]() 的长度,
的长度,
∵∠COH=45°,
∴H转过的圆心角为90°,
∵OM= ![]() ,
,
则弧长= ![]() =
= ![]() =
= ![]() π.
π.
【解析】(1)证明Rt△PMC≌Rt△DMB,即可证明DB=2﹣m,AD=4﹣m,从而求解;(2)分AP=AD,PD=PA,PD=DA三种情况,根据勾股定理即可求解;(3)运动时,路线长不变,可以取当P在O点时,求解即可.