题目内容
【题目】四条线段a,b,c,d如图,a:b:c:d=1:2:3:4 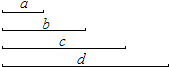
(1)选择其中的三条线段为边作一个三角形(尺规作图,要求保留作图痕迹,不必写出作法);
(2)任取三条线段,求以它们为边能作出三角形的概率.
【答案】
(1)解:只能选b,c,d三边画三角形;
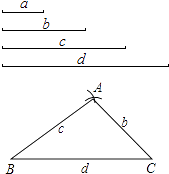
(2)解:
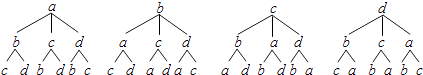
共有24种情况,
能组成三角形的有6种情况,
所求概率为P= ![]()
【解析】(1)选b,c,d三边利用“边边边”作三角形即可;(2)列举出所有情况,看以它们为边能作出三角形的情况数占总情况数的多少即可.
【考点精析】解答此题的关键在于理解三角形三边关系的相关知识,掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边,以及对列表法与树状图法的理解,了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.

练习册系列答案
相关题目




