题目内容
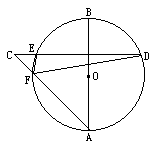
已知:如图,AB为圆O的弦,过点D作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB
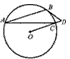
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径等于4,tan∠ACB=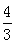 ,求CD的长。
,求CD的长。
(2)若⊙O的半径等于4,tan∠ACB=
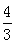 ,求CD的长。
,求CD的长。| 解:(1)直线BD与⊙O相切, 证明:如图,连接OB ∵∠OCB=∠CBD+∠D,∠1=∠D, ∴∠2=∠CBD, ∵AB∥OC, ∴∠2=∠A, ∴∠A=∠CBD, ∵OB=OC, ∴∠BOC+2∠3=180°, ∵∠BOC=2∠A, ∴∠A+∠3=90°, ∴∠CBD+∠3=90°, ∴∠OBD=90°, ∴直线B与⊙O相切; |
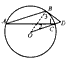 |
| (2)∵∠D=∠ACB·tan∠ACB=4/3, ∴tanD=4/3, 在Rt△OBD中,∠OBD=90°,OB=4,tanD=4/3, ∴sinD=4/5,OD= 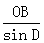 =5 =5∴CD=OD-OC=1。 |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

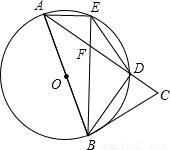
 E交AC于F,
E交AC于F,
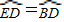 ,BE交AC于F,
,BE交AC于F,