题目内容
【题目】如图,直线AB分别与两坐标轴交于点A(6,0),B(0,12),点C的坐标为(3,0)
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为16,求点P的坐标.
②连结CP,是否存在点P,使△ACP与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)y=﹣2x+12;(2)①点P(2,8)或(4,4);②存在,点P的坐标为(3,6)或点P(![]() ,
,![]() )
)
【解析】
试题(1)由于A(6,0),B(0,12),利用待定系数法即可求出直线AB的解析式;
(2)①可以设动点P(x,﹣2x+12),由此得到PE=x,PF=﹣2x+12,再利用矩形OEPF的面积为16即可求出点P的坐标;
②存在,分两种情况:第一种由CP∥OB得△ACP∽△AOB,由此即可求出P的坐标;第二种CP⊥AB,根据已知条件可以证明APC∽△AOB,然后利用相似三角形的对应边成比例即可求出PA,再过点P作PH⊥x轴,垂足为H,由此得到PH∥OB,进一步得到△APH∽△ABO,然后利用相似三角形的对应边成比例就可以求出点P的坐标.
解:(1)设直线AB的解析式为y=kx+b,如图1:
依题意,![]() ,
,
∴![]() ,
,
∴y=﹣2x+12;
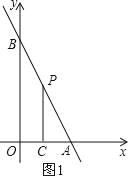
(2)①设动点P (x,﹣2x+12),则PE=x,PF=﹣2x+12,
∴SOEPF=PEPF=x(﹣2x+12)=16,
∴x1=2,x2=4;
经检验x1=2,x2=4都符合题意,
∴点P(2,8)或(4,4);
②存在,分两种情况
∵A(6,0),B(0,12),
∴OA=6,OB=12,AB=6![]()
第一种:CP∥OB,
∴△ACP∽△AOB,
而点C的坐标为(3,0),
∴点P(3,6);
第二种CP⊥AB,
∵∠APC=∠AOB=90°,∠PAC=∠BAO,
∴△APC∽△AOB,
∴![]() ,
,
∴![]() ,
,
∴AP=![]() ,
,
如图2,过点P作PH⊥x轴,垂足为H,
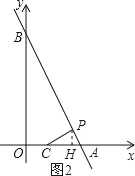
∴PH∥OB,
∴△APH∽△ABO,
∴![]() ,
,
∴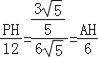 ,
,
∴PH=![]() ,AH=
,AH=![]() ,
,
∴OH=OA﹣AH=6﹣![]() =
=![]() ,
,
∴点P(![]() ,
,![]() ).
).
∴点P的坐标为(3,6)或点P(![]() ,
,![]() ).
).