��Ŀ����
����Ŀ����ͼ1������ȫ�ȵĵȱ���������ͼ���ã��߳�Ϊ4��AC��DE���ڵ�G����D��AB���е㣬BC��DF�ཻ�ڵ�K������GK��
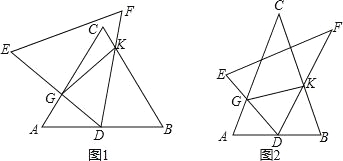
��1��д���������������Σ�����ȫ�ȣ���
��2����֤����GKD=��BKD��
��3������DKG�����ΪS��KG=x��д��S��x�Ĺ�ϵ����д��x��ȡֵ��Χ��
��4�����������е�����ȫ�ȵĵȱ������θ�Ϊ����ȫ�ȵĵ��������Σ�DF=EF=AC=BC������ͼ2�������������䣬ֱ���жϣ�1����2���еĽ����Ƿ���Ȼ������
���𰸡���1����DAG�ס�KBD����KDG�ס�KDB����2��֤���μ���������3��S=![]() x��2��x��3������4��������Ȼ������
x��2��x��3������4��������Ȼ������
��������
�����������1���ɵȱ������ε����ʵó���A=��B=��EDF=60�������������ε�������ʵó���AGD=��BDK�������������֤����DAG�ס�KBD���Ӷ��ó���Ӧ�߳ɱ���![]() ����������ɵ�AD=BD=2���ó�
����������ɵ�AD=BD=2���ó�![]() ���������߶�Ӧ�ɱ������н����֤����KDG�ס�KDB���ɣ���2���ɵȱ������ε����ʵó���A=��B=��EDF=60�������������ε�������ʵó���AGD=��BDK��֤����DAG�ס�KBD���ó���Ӧ�߳ɱ���
���������߶�Ӧ�ɱ������н����֤����KDG�ס�KDB���ɣ���2���ɵȱ������ε����ʵó���A=��B=��EDF=60�������������ε�������ʵó���AGD=��BDK��֤����DAG�ס�KBD���ó���Ӧ�߳ɱ���![]() ����AD=BD=2���ó�
����AD=BD=2���ó�![]() ��֤����KDG�ס�KDB�����ɵó����ۣ���3���ɵ��������ε����ʵó���A=��B=��EDF�����������ε�������ʵó���AGD=��BDK��֤����DAG�ס�KBD���ó���Ӧ�߳ɱ���
��֤����KDG�ס�KDB�����ɵó����ۣ���3���ɵ��������ε����ʵó���A=��B=��EDF�����������ε�������ʵó���AGD=��BDK��֤����DAG�ס�KBD���ó���Ӧ�߳ɱ���![]() ����AD=BD=2���ó�
����AD=BD=2���ó�![]() ��֤����KDG�ס�KDB���Ӷ��õ���DAG�ס�KDG������
��֤����KDG�ס�KDB���Ӷ��õ���DAG�ס�KDG������![]() ����
����![]() ���ó�DGDK=2x����DKG�����S=
���ó�DGDK=2x����DKG�����S=![]() DGDKsin��EDF�����ɵó��������KG��ABʱ��KG��С=
DGDKsin��EDF�����ɵó��������KG��ABʱ��KG��С=![]() AB=2����K��C�غ�ʱ��KG���=3�����ɵó�x��ȡֵ��Χ����4��������Ȼ�������ⷨͬ��1����2�����������������������������֤����DAG�ס�KBD���������߶�Ӧ�ɱ������н������������������֤����KDG�ס�KDB��
AB=2����K��C�غ�ʱ��KG���=3�����ɵó�x��ȡֵ��Χ����4��������Ȼ�������ⷨͬ��1����2�����������������������������֤����DAG�ס�KBD���������߶�Ӧ�ɱ������н������������������֤����KDG�ס�KDB��
�����������1��д�����������ο�������DAG�ס�KBD����KDG�ס�KDB���������£��ߡ�ABC����DEF������ȫ�ȵĵȱ������Σ����A=��B=��EDF=60�����ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF�����AGD=��BDK�����DAG�ס�KBD����![]() ������D��AB���е㣬��AD=BD=2����
������D��AB���е㣬��AD=BD=2����![]() �����KDG�ס�KDB����2��֤�����ߡ�ABC����DEF������ȫ�ȵĵȱ������Σ����A=��B=��EDF=60�����ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF�����AGD=��BDK�����DAG�ס�KBD����
�����KDG�ס�KDB����2��֤�����ߡ�ABC����DEF������ȫ�ȵĵȱ������Σ����A=��B=��EDF=60�����ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF�����AGD=��BDK�����DAG�ס�KBD����![]() ������D��AB���е㣬��AD=BD=2����
������D��AB���е㣬��AD=BD=2����![]() �����ߡ�GDK=��DBK�����KDG�ס�KDB�����GKD=��BKD����3���ɣ�2���ã���DAG�ס�KBD����KDG�ס�KDB�����DAG�ס�KDG����
�����ߡ�GDK=��DBK�����KDG�ס�KDB�����GKD=��BKD����3���ɣ�2���ã���DAG�ס�KBD����KDG�ס�KDB�����DAG�ס�KDG����![]() ����
����![]() ����DGDK=2x�����DKG�����S=
����DGDK=2x�����DKG�����S=![]() DGDKsin��EDF=
DGDKsin��EDF=![]() 2x
2x![]() =
=![]() x����KG��ABʱ��KG��С=
x����KG��ABʱ��KG��С=![]() AB=2����K��C�غ�ʱ��KG���=3����S=
AB=2����K��C�غ�ʱ��KG���=3����S=![]() x��2��x��3������4����1����2���еĽ�����Ȼ�������������£��ߡ�ABC����DEF������ȫ�ȵĵ��������Σ�DF=EF=AC=BC�����A=��B=��EDF���ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF�����AGD=��BDK�����DAG�ס�KBD����
x��2��x��3������4����1����2���еĽ�����Ȼ�������������£��ߡ�ABC����DEF������ȫ�ȵĵ��������Σ�DF=EF=AC=BC�����A=��B=��EDF���ߡ�BDG=��A+��AGD����BDG=��BDK+��EDF�����AGD=��BDK�����DAG�ס�KBD����![]() ������D��AB���е㣬��AD=BD=2����
������D��AB���е㣬��AD=BD=2����![]() �����ߡ�GDK=��DBK�����KDG�ס�KDB�����GKD=��BKD��
�����ߡ�GDK=��DBK�����KDG�ס�KDB�����GKD=��BKD��

����Ŀ��ij��������������������A�����������ͺ����飬����������Ϊ������ʻ������ʻ�����У������������y����������ʻʱ��t��Сʱ��֮��Ĺ�ϵ���±���
t��Сʱ�� | 0 | 1 | 2 | 3 |
y������ | 100 | 92 | 84 | 76 |
�ɱ�����y��t�Ĺ�ϵ��֪����������ʻ________Сʱ�������������Ϊ0��