题目内容
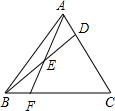 如图△ABC中,D点在AC上,AD:DC=1:2,连BD,E是BD的中点,延长AE交BC于F,则BF:FC的比是
如图△ABC中,D点在AC上,AD:DC=1:2,连BD,E是BD的中点,延长AE交BC于F,则BF:FC的比是
- A.

- B.

- C.

- D.

B
分析:过E作BC的平行线交AC与G,由中位线的知识可得出AD:DC=1:2,根据已知和平行线分线段成比例得出AD=DG=GC,
AG:GC=2:1,AE:EF=2:1,再由同高不同底的三角形中底与三角形面积的关系可求出BF:FC的比.
解答: 解:如图,过E作EG∥BC,交AC于G,
解:如图,过E作EG∥BC,交AC于G,
∵E是BD的中点,
∴G是DC的中点.
又AD:DC=1:2,
∴AD=DG=GC,
∴AG:GC=2:1,AE:EF=2:1,
∴S△AEB:S△BEF=2
设S△BEF=S,S△AEB=2S,又BE=ED,
∴S△AED=2S,S△ABD=4S,
∵AD:DC=1:2,
∴S△BDC=2S△ABD=8S,S四边形CDEF=7S,
∴S△AFC=9S,S△ABF=3S,
∴ =
=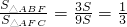 .
.
故选B.
点评:本题考查平行线分线段成比例及三角形的中位线的知识,难度较大,注意熟练运用中位线定理和三角形面积公式.
分析:过E作BC的平行线交AC与G,由中位线的知识可得出AD:DC=1:2,根据已知和平行线分线段成比例得出AD=DG=GC,
AG:GC=2:1,AE:EF=2:1,再由同高不同底的三角形中底与三角形面积的关系可求出BF:FC的比.
解答:
 解:如图,过E作EG∥BC,交AC于G,
解:如图,过E作EG∥BC,交AC于G,∵E是BD的中点,
∴G是DC的中点.
又AD:DC=1:2,
∴AD=DG=GC,
∴AG:GC=2:1,AE:EF=2:1,
∴S△AEB:S△BEF=2
设S△BEF=S,S△AEB=2S,又BE=ED,
∴S△AED=2S,S△ABD=4S,
∵AD:DC=1:2,
∴S△BDC=2S△ABD=8S,S四边形CDEF=7S,
∴S△AFC=9S,S△ABF=3S,
∴
 =
=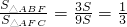 .
.故选B.
点评:本题考查平行线分线段成比例及三角形的中位线的知识,难度较大,注意熟练运用中位线定理和三角形面积公式.

练习册系列答案
相关题目
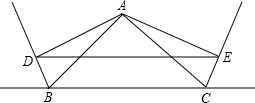 如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.

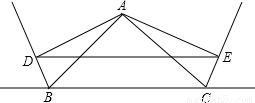 如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.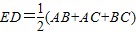 .
.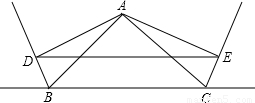 如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.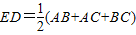 .
.