题目内容
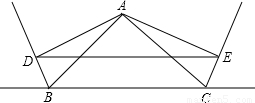
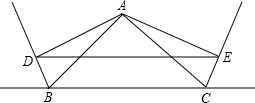 如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.求证:(1)ED∥BC;
(2)ED=
| 1 | 2 |
分析:(1)分别延长AD、AE与直线BC交于点F、G,根据AD⊥BD,得到∠ADB=∠FDB=90°,再根据BD=BD,∠ABD=∠FBD,证得△ABD≌△FBD,进而得到AD=FD、AE=EG,证得DE∥BC.
(2)根据上题证得的△ABD≌△FBD,AB=BF,同理AC=CG,证得GF=FB+BC+GC=AB+BC+AC,从而证得结论.
(2)根据上题证得的△ABD≌△FBD,AB=BF,同理AC=CG,证得GF=FB+BC+GC=AB+BC+AC,从而证得结论.
解答:证明:(1)分别延长AD、AE与直线BC交于点F、G,
∵AD⊥BD,
∴∠ADB=∠FDB=90°,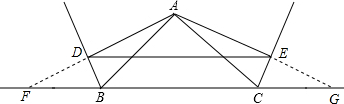
∵BD=BD,∠ABD=∠FBD,
∴△ABD≌△FBD
∴AD=FD,
同理可得AE=EG,
∴DE∥BC;
(2)由(1)知△ABD≌△FBD,
∴AB=BF,
同理AC=CG,
∵DE=
FG
∴GF=FB+BC+GC=AB+BC+AC,
∴DE=
(AB+BC+AC).
∵AD⊥BD,
∴∠ADB=∠FDB=90°,

∵BD=BD,∠ABD=∠FBD,
∴△ABD≌△FBD
∴AD=FD,
同理可得AE=EG,
∴DE∥BC;
(2)由(1)知△ABD≌△FBD,
∴AB=BF,
同理AC=CG,
∵DE=
| 1 |
| 2 |
∴GF=FB+BC+GC=AB+BC+AC,
∴DE=
| 1 |
| 2 |
点评:本题考查了三角形的中位线定理及三角形的有关知识,解题的关键是正确的利用中位线定理得到中位线与第三边的位置或数量关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
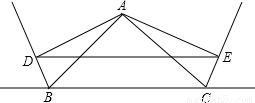 如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.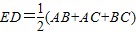 .
. 如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.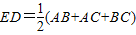 .
.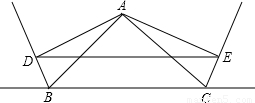 如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.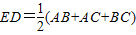 .
.