题目内容
(2013•惠山区一模)(1)解方程:3x2-6x-1=0;
(2)解不等式组:
.
(2)解不等式组:
|
分析:(1)先计算出△=(-6)2-4×3×(-1)=48,然后代入一元二次方程的求根公式中进行计算;
(2)分别解两个不等式得到x≥-1和x≤3,然后根据“大于小的小于大的取中间”即可得到不等式组的解集.
(2)分别解两个不等式得到x≥-1和x≤3,然后根据“大于小的小于大的取中间”即可得到不等式组的解集.
解答:(1)解:∵a=3,b=-6,c=-1,
∴△=(-6)2-4×3×(-1)=48,
∴x=
=
=
,
∴x1=
,x2=
;
(2)
,
由①得x≥-1,
由②得x≤3,
∴-1≤x≤3.
∴△=(-6)2-4×3×(-1)=48,
∴x=
6±
| ||
| 2×3 |
6±4
| ||
| 6 |
3±2
| ||
| 3 |
∴x1=
3+2
| ||
| 3 |
3-2
| ||
| 3 |
(2)
|
由①得x≥-1,
由②得x≤3,
∴-1≤x≤3.
点评:本题解一元二次方程-公式法:一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0)的求根公式为x=
(b2-4ac≥0).也考查了解一元一次不等式组.
-b±
| ||
| 2a |

练习册系列答案
相关题目
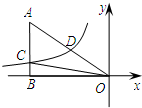 (2013•惠山区一模)如图,已知双曲线
(2013•惠山区一模)如图,已知双曲线