题目内容
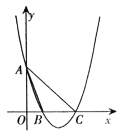
【题目】如图,在平面直角坐标系中,⊙O的半径为1,点A在x轴的正半轴上,B为⊙O上一点,过点A、B的直线与y轴交于点C,且OA2=ABAC.

(1)求证:直线AB是⊙O的切线;
(2)若AB=![]() ,求直线AB对应的函数表达式.
,求直线AB对应的函数表达式.
【答案】(1)见解析;(2)![]()
【解析】
,
(1)连接OB,根据题意可证明△OAB∽△CAO,继而可推出OB⊥AB,根据切线定理即可求证结论;
(2)根据勾股定理可求得OA=2及A点坐标,根据相似三角形的性质可得![]() ,进而可求CO的长及C点坐标,利用待定系数法,设直线AB对应的函数表达式为y=kx+b,再把点A、C的坐标代入求得k、b的值即可.
,进而可求CO的长及C点坐标,利用待定系数法,设直线AB对应的函数表达式为y=kx+b,再把点A、C的坐标代入求得k、b的值即可.
(1)证明:连接OB.
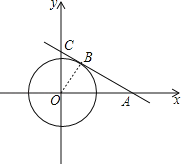
∵OA2=ABAC
∴![]() ,
,
又∵∠OAB=∠CAO,
∴△OAB∽△CAO,
∴∠ABO=∠AOC,
又∵∠AOC=90°,
∴∠ABO=90°,
∴AB⊥OB;
∴直线AB是⊙O的切线;
(2)解:∵∠ABO=90°,![]() ,OB=1,
,OB=1,
∴![]() ,
,
∴点A坐标为(2,0),
∵△OAB∽△CAO,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴点C坐标为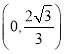 ;
;
设直线AB对应的函数表达式为y=kx+b,
则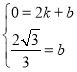 ,
,
∴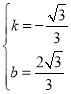
∴![]() .
.
即直线AB对应的函数表达式为![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;