题目内容
(本题满分12分)我们设想用电脑模拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。(1)希望A球撞击桌边上C点后反弹,再击中B球,请给出一个算法,告知电脑怎样找到点C,并求出C点的坐标。
(2)设桌边RQ上有一球袋S(100,120),判定6号球B被从C点反弹出的白球撞击后能否直接落入球袋S中,(假定6号球被撞后速度足够大)。
(3)若用白球A直接击打6号球B,使6号球B撞击桌边OP上的D点后反弹,问6号球B从D点反弹后能否直接进入球袋Q中?(假定6号球被撞后速度足够大)

(1)作A点关于x轴的对称A',连结BA'交x轴于一点,这一点就是C点,由A(40,60),A'(40,-60),设直线BA'的解析式为y=kx+b,于是有
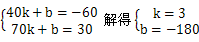
∴y=3x-180,令y=0,有x=60,故C(60,0).
(2)当x=100时,y=3×100-180=120,所以点S(100,120)在直线y=3x-180上,即6号球能落入S球袋中。
(3)设直线AB的解析式为y=kx+b,则有
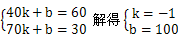
∴ y=-x+100,令y=0,x=100,则D(100,0),作AM⊥x轴于M,则AM=DM=60。
∴∠a=45°,由约定可知,∠β=45°,则反弹后直线DP平行于y=x,且过(100,0),则直线DP方程为y=x-100,当x=200时,y=100,故Q(200,120)不在该直线上,6号球从D处反弹后不能直接落入Q球袋中。
(1)作A点关于x轴的对称A',连结BA'交x轴于一点,这一点就是C点,由A(40,60),A'(40,-60),设直线BA'的解析式为y=kx+b,于是有
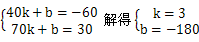
∴y=3x-180,令y=0,有x=60,故C(60,0).
(2)当x=100时,y=3×100-180=120,所以点S(100,120)在直线y=3x-180上,即6号球能落入S球袋中。
(3)设直线AB的解析式为y=kx+b,则有
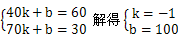
∴ y=-x+100,令y=0,x=100,则D(100,0),作AM⊥x轴于M,则AM=DM=60。
∴∠a=45°,由约定可知,∠β=45°,则反弹后直线DP平行于y=x,且过(100,0),则直线DP方程为y=x-100,当x=200时,y=100,故Q(200,120)不在该直线上,6号球从D处反弹后不能直接落入Q球袋中。解析:
略
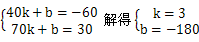
∴y=3x-180,令y=0,有x=60,故C(60,0).
(2)当x=100时,y=3×100-180=120,所以点S(100,120)在直线y=3x-180上,即6号球能落入S球袋中。
(3)设直线AB的解析式为y=kx+b,则有
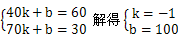
∴ y=-x+100,令y=0,x=100,则D(100,0),作AM⊥x轴于M,则AM=DM=60。
∴∠a=45°,由约定可知,∠β=45°,则反弹后直线DP平行于y=x,且过(100,0),则直线DP方程为y=x-100,当x=200时,y=100,故Q(200,120)不在该直线上,6号球从D处反弹后不能直接落入Q球袋中。
(1)作A点关于x轴的对称A',连结BA'交x轴于一点,这一点就是C点,由A(40,60),A'(40,-60),设直线BA'的解析式为y=kx+b,于是有
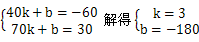
∴y=3x-180,令y=0,有x=60,故C(60,0).
(2)当x=100时,y=3×100-180=120,所以点S(100,120)在直线y=3x-180上,即6号球能落入S球袋中。
(3)设直线AB的解析式为y=kx+b,则有
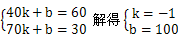
∴ y=-x+100,令y=0,x=100,则D(100,0),作AM⊥x轴于M,则AM=DM=60。
∴∠a=45°,由约定可知,∠β=45°,则反弹后直线DP平行于y=x,且过(100,0),则直线DP方程为y=x-100,当x=200时,y=100,故Q(200,120)不在该直线上,6号球从D处反弹后不能直接落入Q球袋中。解析:
略

练习册系列答案
相关题目
 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元, 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元,
 时,
时, 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元,
 时,
时, 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元,
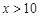 时,
时,