题目内容
【题目】如图,![]() 两村在一条小河的同一侧,要在河边建水厂向两村供水.
两村在一条小河的同一侧,要在河边建水厂向两村供水.
(1)若要使自来水厂到两村的距离相等,厂址![]() 应选在哪个位置?
应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址![]() 应选在哪个位置?
应选在哪个位置?
(3)自来水厂建好后,在招收职工的试卷中有道题“请你在河流![]() 上找出一点
上找出一点![]() ,使
,使![]() 的值最大.”你能找到
的值最大.”你能找到![]() 点吗?请将上述
点吗?请将上述![]() 三点在下列各图分别标出,并保留尺规作图痕迹.
三点在下列各图分别标出,并保留尺规作图痕迹.

【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)根据垂直平分线的性质可得M在AB的垂直平分线和CD 的交点处;
(2)首先作出A关于河的对称点A′,再连接A′B,与河的交点就是N位置;
(3)根据两边之差小于第三边得到P位于AB与CD交点处时,|PA-PB|最大;
解:(1)∵自来水厂到两村的距离相等,即MA=MB,
∴M在AB的垂直平分线上,如图:
厂址应该选在M处;
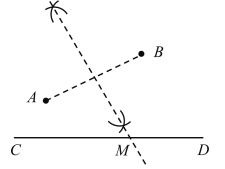
(2)由题意可知,若自来水厂到两村的输水管用料最省,即AN+BN最小,
如图,A′为点A关于CD的对称点,连接A′B,与CD交于点N,
则厂址应该选在点N处;
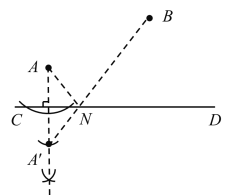
(3)若![]() 最大,根据三角形两边之差小于第三边,如图,
最大,根据三角形两边之差小于第三边,如图,
可知P位于AB与CD交点处时,|PA-PB|最大;

练习册系列答案
相关题目