题目内容
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E,F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.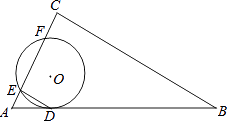
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
【答案】
(1)解:连接OD、OE,
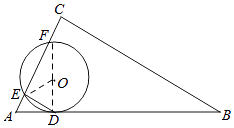
设∠EOD=n°,
∵弧DE的长度为2π,
∴2π= ![]() ,
,
∴n=60°,
∴△EOD是等边三角形,
∴∠ODE=60°,
∵AB是⊙O的切线,
∴∠ODA=90°
∴∠EAD=30°,
∴∠B=∠EAD,
∴ED∥BC,
(2)解:连接FD,
由(1)可知ED∥BC,
∴∠AED=∠C=90°,
∴由圆周角定理可知:FD是⊙O的直径,
∴∠AFD=30°,
∴cos∠AFD= ![]() ,DF=12
,DF=12
∴AF=8 ![]() ,
,
∵cos∠AFD= ![]() ,
,
∴EF=6 ![]() ,
,
∴CE=AF=8 ![]() ,
,
∴AE=CF=2 ![]() ,
,
∴AC=10 ![]() ,
,
∵tanB= ![]() ,
,
∴BC=30,
【解析】(1)根据弧长公式求出n的度数,得到△EOD是等边三角形,由AB是⊙O的切线,得到∠B=∠EAD,由平行线的判定方法得出ED∥BC;(2)由圆周角定理可知FD是⊙O的直径,由特殊角的函数值,求出EF、CE=AF、AE=CF、AC的值,由三角函数求出BC的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目