题目内容
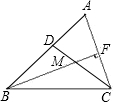已知：如图，CD平分∠ACB，BF是△ABC的高，若∠A=80°，∠ABC=50°，
求∠BMC的度数．
解：∵∠A=80°，∠ABC=50°，
∴∠ACB=50°．
∵CD平分∠ACB，BF⊥AC，
∴∠MCF=25°，∠MFC=90°，
∴∠BMC=∠MCF+∠MFC=25°+90°=115°．
分析：因为∠A=80°，∠ABC=50°，由三角形内角和定理可知∠ACB=50°，又因为CD平分∠ACB，BF是△ABC的高，所以∠MCF=25°，∠MFC=90°，由三角形外角性质可得∠BMC=∠MCF+∠MFC．
点评：本题考查了同学们利用角平分线的性质解决问题的能力，有利于培养同学们的思维能力．
∴∠ACB=50°．
∵CD平分∠ACB，BF⊥AC，
∴∠MCF=25°，∠MFC=90°，
∴∠BMC=∠MCF+∠MFC=25°+90°=115°．
分析：因为∠A=80°，∠ABC=50°，由三角形内角和定理可知∠ACB=50°，又因为CD平分∠ACB，BF是△ABC的高，所以∠MCF=25°，∠MFC=90°，由三角形外角性质可得∠BMC=∠MCF+∠MFC．
点评：本题考查了同学们利用角平分线的性质解决问题的能力，有利于培养同学们的思维能力．
练习册系列答案
相关题目
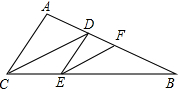
22、已知，如图，CD平分∠ACB，AC∥DE，CD∥EF，求证：EF平分∠DEB．
23、已知：如图，CD平分∠ACB，BF是△ABC的高，若∠A=80°，∠ABC=50°，
