题目内容
一次函数y=ax+b的图象与反比例函数y=
的图象交于A(1,4)、B(-2,m)两点,
(1)求一次函数和反比例函数的关系式;
(2)画出草图,并据此写出使一次函数值大于反比例函数值的x的取值范围;
(3)试求由坐标原点O及点A、点B所围成的三角形的面积.
| k | x |
(1)求一次函数和反比例函数的关系式;
(2)画出草图,并据此写出使一次函数值大于反比例函数值的x的取值范围;
(3)试求由坐标原点O及点A、点B所围成的三角形的面积.
分析:(1)把A(1,4)代入y=
求出反比例函数的关系式,把B(-2,m)代入y=
求出B的坐标,把A、B的坐标代入y=ax+b得出方程,即可求出一次函数的解析式.
(2)画出图象,结合图象和A、B的坐标求出即可.
(3)求出C的坐标,根据三角形面积公式求出即可.
| k |
| x |
| 4 |
| x |
(2)画出图象,结合图象和A、B的坐标求出即可.
(3)求出C的坐标,根据三角形面积公式求出即可.
解答:解:(1)把A(1,4)代入y=
得:k=4,
即反比例函数的关系式是:y=
,
把B(-2,m)代入y=
得:m=-2,
即B的坐标是(-2,-2),
把A、B的坐标代入y=ax+b得:
,
解得:a=2,b=2,
即一次函数的关系式是y=2x+2.
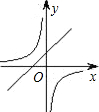
(2)如图:

一次函数值大于反比例函数值的x的取值范围是-2<x<0或x>1.
(3)
连接OA、OB,
当y=0时,2x+2=0,
解得:x=-1,
即OC=1,
∴△AOB的面积S=S△AOC+S△BOC=
×1×4+
×1×2=3.
| k |
| x |
即反比例函数的关系式是:y=
| 4 |
| x |
把B(-2,m)代入y=
| 4 |
| x |
即B的坐标是(-2,-2),
把A、B的坐标代入y=ax+b得:
|
解得:a=2,b=2,
即一次函数的关系式是y=2x+2.
(2)如图:

一次函数值大于反比例函数值的x的取值范围是-2<x<0或x>1.
(3)

连接OA、OB,
当y=0时,2x+2=0,
解得:x=-1,
即OC=1,
∴△AOB的面积S=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一次函数和反比例函数的交点问题,函数的图象,用待定系数法求反比例函数的解析式的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
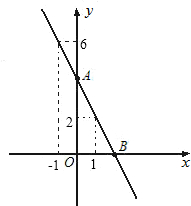 已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求:
已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求: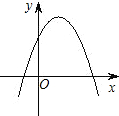 已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=
已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=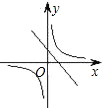
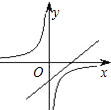
 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=