题目内容
【题目】阅读下列材料:
已知:如图1,直线AB∥CD,点E是AB、CD之间的一点,连接BE、DE得到∠BED.
求证:∠BED =∠B+∠D.
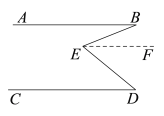 图1
图1
小冰是这样做的:
证明:过点E作EF∥AB,则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF +∠FED =∠B+∠D.
即∠BED=∠B+∠D.
请利用材料中的结论,完成下面的问题:
已知:直线 AB∥CD,直线MN分别与AB、CD交于点E、F.
(1)如图2,∠BEF和∠EFD的平分线交于点G.猜想∠G的度数,并证明你的猜想;
(2)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2.求证:∠FG1 E+∠G2=180°.


【答案】(1)猜想:∠EGF=90°.证明见解析;(2)证明见解析.
【解析】
(1)如图2所示,猜想:∠EGF=90°;由结论(1)得∠EGF=∠BEG+∠GFD,根据EG、FG分别平分∠BEF和∠EFD,得到∠BEF=2∠BEG,∠EFD=2∠GFD,由于BE∥CF到∠BEF+∠EFD=180°,于是得到2∠BEG+2∠GFD=180°,即可得到结论;
(2)如图3,过点G1作G1H∥AB由结论(1)可得∠G2=∠1+∠3,∠EG1F=∠BEG1+∠G1FD,得到∠3=∠G2FD,由于FG2平分∠EFD求得∠4=∠G2FD,由于∠1=∠2,于是得到∠G2=∠2+∠4,由于∠EG1F=∠BEG1+∠G1FD,得到∠EG1F+∠G2=∠2+∠4+∠BEG1+∠G1FD=∠BEF+∠EFD,然后根据平行线的性质即可得到结论.
(1)猜想:∠EGF=90°.
证明:∵ EG,FG分别平分∠BEF和∠EFD,
∴∠BEF =2∠BEG,∠EFD=2∠GFD.
∵BE//CF,
∴∠BEF +∠EFD=180°.
∴2∠BEG+2∠GFD=180°.
∴∠BEG+∠GFD=90°.
∵由小冰的结论可得∠EGF =∠BEG+∠GFD,
∴∠EGF=90°.
(2)证明:过点G1作G1H//AB,
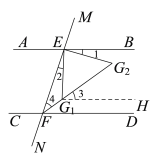
∵AB//CD,
∴G1H//CD.
∴∠3=∠G2FD.
∵由小冰的结论可得∠G2 =∠1+∠3,
∵FG2平分∠EFD,
∴∠4=∠G2FD.
∵∠1=∠2,
∴∠G2=∠2+∠4.
∵由小冰的结论可得∠EG1F =∠BEG1+∠G1FD,
∴∠EG1F +∠G2 =∠BEG1+∠G1FD+∠2+∠4
=∠BEF+∠EFD
=180°.