题目内容
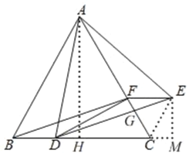
【题目】如图，等边三角形ABC的边长是6，点D、F分别是BC、AC上的动点，且BD＝CF，以AD为边作等边三角形ADE，连接BF、EF．
（1）求证：四边形BDEF是平行四边形；
（2）连接DF，当BD的长为何值时，△CDF为直角三角形？
（3）设BD＝x，请用含x的式子表示等边三角形ADE的面积．
【答案】（1）见解析；（2）BD＝2或4；（3）S△ADE＝
（x﹣3）2+
（0≤x≤6）
【解析】
(1)：要证明四边形BDEF是平行四边形，一般采用对边平行且相等来证明，因为已经有了DB=CF，只要有△ABD全等△ACE，就能得到∠ACE=∠ABD=60°，CE=CF=EF=BD，再利用∠CFE＝60°＝∠ACB，就能平行，故第一问的证；
(2)：反推法，当△CDF为直角三角形，又因为∠C=60°，当∠CDF=90°时，可以知道
2CD=CF，因为CF=BD，BD+CD=6，∴BD=4，当∠CFD=90°时，可以知道CD=2CF，因为CF=BD，BD+CD=6，∴BD=2，故当BD=2或4时，△CFD为直角三角形；
(3)：求等边三角形ADE的面积，只要知道边长就可求出，但是AD是变化的，所以我们采用组合面积求解，利用四边形ADCE减去△CDE即可，又因为△ABD≌△ACE，所以四边形ADCE的面积等于△ABD的面积，所以只需要求出△ABC的面积与△CDE即可,从而即可求面积.
解：（1）
∵△ABC是等边三角形，
∴AB＝BC，∠BAC＝∠ABD＝∠BCF＝60°，
∵BD＝CF，
∴△ABD≌△BCF（SAS），
∴BD＝CF，
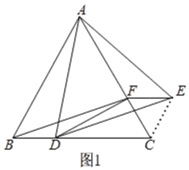
如图1，连接CE，∵△ADE是等边三角形，
∴AD＝AE，∠DAE＝60°，
∴∠BAD＝∠CAE，
∵AB＝AC，
∴△ABD≌△ACE（SAS），
∴∠ACE＝∠ABD＝60°，BD＝CE，
∴CF＝CE，
∴△CEF是等边三角形，
∴EF＝CF＝BD，∠CFE＝60°＝∠ACB，
∴EF∥BC，
∵BD＝EF，
∴四边形BDEF是平行四边形；
（2）∵△CDF为直角三角形，
∴∠CFD＝90°或∠CDF＝90°，
当∠CFD＝90°时，∵∠ACB＝60°，
∴∠CDF＝30°，
∴CD＝2CF，
由（1）知，CF＝BD，
∴CD＝2BD，
即：BC＝3BD＝6，
∴BD＝2，
∴x＝2，
当∠CDF＝90°时，∵∠ACB＝60°，
∴∠CFD＝30°，
∴CF＝2CD，
∵CF＝BD，
∴BD＝2CD，
∴BC＝3CD＝6，
∴CD＝2，
∴x＝BD＝4，
即：BD＝2或4时，△CDF为直角三角形；
（3）如图，
连接CE，由（1）△ABD≌△ACE，
∴S△ABD＝S△ACE，BD＝CE，
∵BD＝CF，
∴△CEF是等边三角形，
∴EM＝
CE＝x，
∴S△CDE＝
CD×EM＝（6﹣x）×x＝x（6﹣x）
∴BH＝CH＝BC＝3，
∴AH＝3
，
∴S△ABC＝BCAH＝9
∴S△ADE＝S四边形ADCE﹣S△CDE
＝S△ACD+S△ACE﹣S△CDE
＝S△ACD+S△ABD﹣S△CDE
＝S△ABC﹣S△CDE
＝9﹣x（6﹣x）
＝（x﹣3）2+（0≤x≤6）
