题目内容
(2005•滨州)在△ABC中,若∠A、∠B、∠C的对边分别为a、b、c,则有结论:a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC;
(Ⅰ)上面的结论即为著名的余弦定理,试用文字语言表述余弦定理:______;
试用余弦定理解答下面的问题(Ⅱ):
(Ⅱ)过边长为1的正三角形的中心O引两条夹角为120°的射线,分别与正三角形的边交于M、N两点,试求线段MN长的取值范围(借助图解答).

【答案】分析:(1)等号左边是一边的平方,等号右边前两项是其他两边的平方和减去2倍的这2边与它们夹角余弦值的积.
(2)易得△CNO≌△AMO,那么可得到相对应的边相等,利用(1)的结论在△MCN中表示出MN的值,利用二次函数求得最值,利用所给范围得到相应的范围值.
解答: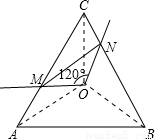 解:(Ⅰ)三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
解:(Ⅰ)三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
(Ⅱ)如图,设AM=x,则CN=x,MC=1-x,0≤x≤1,
在△MCN中,∠MCN=60°,
由余弦定理,得
MN=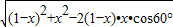 ,
,
= =
=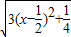 ,
,
∵0≤x≤1,
∴当x= 时,MN取最小值
时,MN取最小值 ,
,
当x=0,1时,MN取最大值1,
∴ ≤MN≤1.
≤MN≤1.
点评:应先找易表示出各边的,所求线段所在的三角形,注意运用已得到的结论进行证明.
(2)易得△CNO≌△AMO,那么可得到相对应的边相等,利用(1)的结论在△MCN中表示出MN的值,利用二次函数求得最值,利用所给范围得到相应的范围值.
解答:
 解:(Ⅰ)三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
解:(Ⅰ)三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.(Ⅱ)如图,设AM=x,则CN=x,MC=1-x,0≤x≤1,
在△MCN中,∠MCN=60°,
由余弦定理,得
MN=
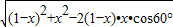 ,
,=
 =
=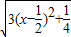 ,
,∵0≤x≤1,
∴当x=
 时,MN取最小值
时,MN取最小值 ,
,当x=0,1时,MN取最大值1,
∴
 ≤MN≤1.
≤MN≤1.点评:应先找易表示出各边的,所求线段所在的三角形,注意运用已得到的结论进行证明.

练习册系列答案
相关题目
 ).
). ).
).


