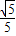题目内容
(2005•滨州)在平面直角坐标系xOy中,已知点A(-1,0),B(0,1),C(2, ).
).(Ⅰ)直线l:y=kx+b过A、B两点,求k、b的值;
(Ⅱ)求过A、B、C三点的抛物线Q的解析式;
(Ⅲ)设(Ⅱ)中的抛物线Q的对称轴与x轴相交于点E,那么在对称轴上是否存在点F,使⊙F与直线l和x轴同时相切?若存在,求出点F的坐标;若不存在,请说明理由.
【答案】分析:(1)直线l:y=kx+b过A、B两点,把这两点的坐标代入函数解析式,就可以得到关于k,b的方程组,就可以求出k,b的值.
(2)A、B、C三点的坐标已知,根据待定系数法就可以求出函数的解析式.
(3)对称轴上是否存在点F,使⊙F与直线l和x轴同时相切,应分F在x轴的上方和下方两种情况进行讨论.当F在x轴的上方时,设直线l与x轴的交点是P,则PF是三角形MPE的角平分线,根据三角形角平分线的性质就可以求出F的坐标.
当F在x轴的下方时,△MNF为等腰直角三角形.根据等腰直角三角形的性质就可以求出F点的坐标.
解答: 解:(Ⅰ)∵直线y=kx+b过A、B两点,
解:(Ⅰ)∵直线y=kx+b过A、B两点,
∴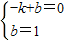 (1分)
(1分)
解这个方程组,
得k=1,b=1.(2分)
(Ⅱ)设抛物线的解析式为y=ax2+bx+c,
则有: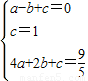 (3分)
(3分)
解这个方程组,
得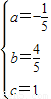
∴抛物线的解析式为y=- x2+
x2+ x+1.(4分)
x+1.(4分)
(Ⅲ)存在⊙F与直线l和x轴同时相切.
易知抛物线Q的对称轴为x=2,(5分)
①当圆心F在x轴的上方时,
设点F的坐标为(2,y),把x=2代入y=x+1,
得y=3.
∴抛物线Q的对称轴与直线l的交点为M(2,3).(6分)
∴EF=y,ME=3,MF=ME-EF=3-y.(7分)
由直线l:y=x+1知,
∠NMF=45度.
∴△MNF是等腰直角三角形
∴MF=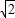 NF=
NF=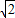 EF
EF
∴3-y=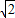 y
y
∴y=3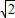 -3
-3
∴点F的坐标为(2,3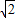 -3).(8分)
-3).(8分)
②当圆心F在x轴的下方时,设点F的坐标为(2,y),则MF=3-y,FE=-y.
由△MNF为等腰直角三角形,得3-y= y,(9分)
y,(9分)
∴y=-3-3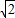
∴点F的坐标为(2,-3-3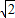 ).(10分)
).(10分)
点评:本题主要考查了待定系数法求函数的解析式.利用数形结合的方法解决本题,理解图形中圆与直线的关系是解题的关键.
(2)A、B、C三点的坐标已知,根据待定系数法就可以求出函数的解析式.
(3)对称轴上是否存在点F,使⊙F与直线l和x轴同时相切,应分F在x轴的上方和下方两种情况进行讨论.当F在x轴的上方时,设直线l与x轴的交点是P,则PF是三角形MPE的角平分线,根据三角形角平分线的性质就可以求出F的坐标.
当F在x轴的下方时,△MNF为等腰直角三角形.根据等腰直角三角形的性质就可以求出F点的坐标.
解答:
 解:(Ⅰ)∵直线y=kx+b过A、B两点,
解:(Ⅰ)∵直线y=kx+b过A、B两点,∴
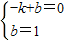 (1分)
(1分)解这个方程组,
得k=1,b=1.(2分)
(Ⅱ)设抛物线的解析式为y=ax2+bx+c,
则有:
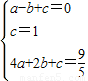 (3分)
(3分)解这个方程组,
得
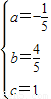
∴抛物线的解析式为y=-
 x2+
x2+ x+1.(4分)
x+1.(4分)(Ⅲ)存在⊙F与直线l和x轴同时相切.
易知抛物线Q的对称轴为x=2,(5分)
①当圆心F在x轴的上方时,
设点F的坐标为(2,y),把x=2代入y=x+1,
得y=3.
∴抛物线Q的对称轴与直线l的交点为M(2,3).(6分)
∴EF=y,ME=3,MF=ME-EF=3-y.(7分)
由直线l:y=x+1知,
∠NMF=45度.
∴△MNF是等腰直角三角形
∴MF=
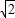 NF=
NF=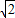 EF
EF∴3-y=
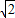 y
y∴y=3
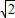 -3
-3∴点F的坐标为(2,3
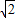 -3).(8分)
-3).(8分)②当圆心F在x轴的下方时,设点F的坐标为(2,y),则MF=3-y,FE=-y.
由△MNF为等腰直角三角形,得3-y=
 y,(9分)
y,(9分)∴y=-3-3
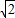
∴点F的坐标为(2,-3-3
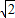 ).(10分)
).(10分)点评:本题主要考查了待定系数法求函数的解析式.利用数形结合的方法解决本题,理解图形中圆与直线的关系是解题的关键.

练习册系列答案
相关题目
 ).
).